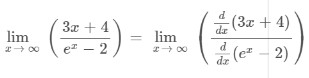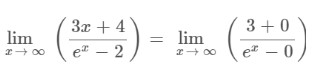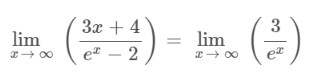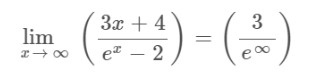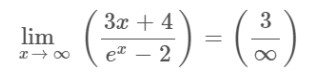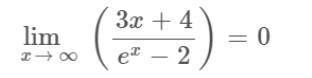L'hopital's Rule Calculator

L'hopital's Rule Calculator

L’hopital’s rule calculator is used to find the limits of indeterminate functions. This L’hopital’s calculator provides the result of undefined functions in the form of 0/0 or ∞/∞ with steps. 

What is L’hopital’s rule?

L’hopital’s rule is a theorem of limit used to evaluate the limit of indeterminate forms. The indeterminate forms are expressions of the form of 0/0, 0⁰, 0 x (±∞), ∞ - ∞, 1^∞, ∞⁰, and ∞/∞ after computing limits.  

Equation of L'hopital's rule

L’hopital’s rule states that if f(x) & g(x) are differentiable functions and d/dx [g(x)] ≠ 0 on an open interval. If one of the following terms is true. 

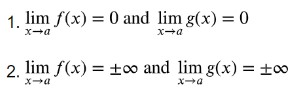
 Then the L’hopital’s rule must be applied

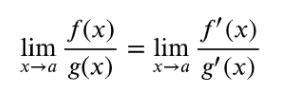
How to evaluate limits using L’hopital’s rule?

Below is a solved example of L’hopital’s rule to evaluate limits.

Example 

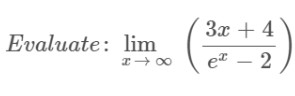
Solution 

Step 1: Apply the limit x→∞ to the above expression.
 
 

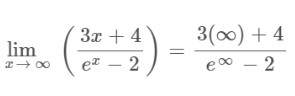
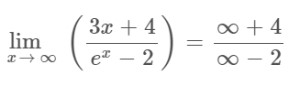
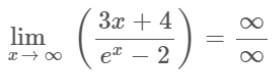
 Step 2: Apply L’hopital’s rule as it gives an indeterminate form after applying the limit.