To calculate result you have to disable your ad blocker first.
Limit Calculator
Enter the function & limit in the fields below, select the variable, and hit submit button to solve the limit using limits calculator.
Limit Calculator with steps
Limit calculator is an online tool that evaluates limits for the given functions and shows all steps. It solves limits with respect to a variable. Limits can be evaluated on either left or right hand side using this limit solver.
What are Limits?
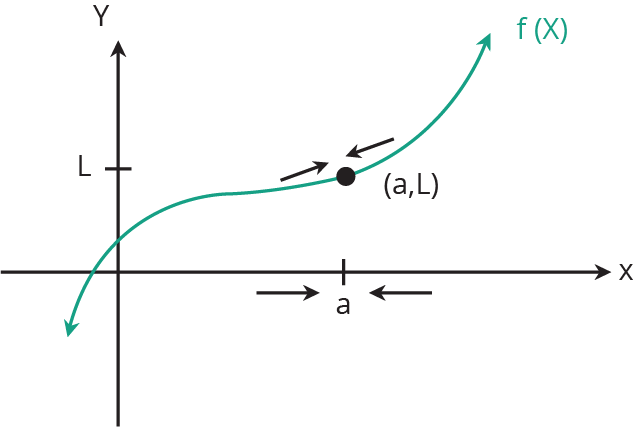
“The limit of a function is the value that f(x) gets closer to as x approaches some number.”
Limx→b [f(x)] = L
Limits are vital to mathematical analysis and calculus. They are also used to define derivatives, integrals, and continuity.
Rules of Limits
Here are some well-known rules/laws/properties of limits.
| Rules | Expressions |
| Sum/Difference Rule | limx→b[f(x) ± h(x)] = limx→b[f(x)] ± limx→b[h(x)] |
| Power Rule | limx→b[f(x)n] = [limx→b[f(x)]]n |
| Product Rule | limx→b[f(x) * h(x)] = limx→b[f(x)] * limx→b[h(x)] |
| Constant Rule | limx→b[k] = k |
| Quotient Rule | limx→b[f(x) / h(x)] = limx→b[f(x)] / limx→b[h(x)] |
| L'Hopital's Rule | limx→b[f(x) / h(x)] = limx→b[f'(x) /h'(x)] |
How to evaluate Limits?
Using the online limit calculator is the best way to solve limits, however, we will discuss the manual method to evaluate limits. Follow the below example to understand step by step method to solve limits.
Example:
Find the limit:
Iimx→2(x3 + 4x2 − 2x + 1)
Step 1: Apply the limit function separately to each value.
= Iimx→2(x3) + Iimx→2(4x2) - Iimx→2(2x) + lIimx→2(1)
Step 2: Separate coefficients and get them out of the limit function.
= Iimx→2(x3) + 4 Iimx→2(x2) - 2 Iimx→2(x) + Iimx→2(1)
Step 3: Apply the limit value by substituting x = 2 in the equation to find the limit.
Iimx→2(x3 + 4x2 − 2x + 1) = 1(23) + 4(22) – 2(2) + 1
Iimx→2(x3 + 4x2 − 2x + 1) = 8 + 16 – 4 + 1
Iimx→2(x3 + 4x2 − 2x + 1) = 21
The limit finder above also uses L'hopital's rule to solve limits.
You can also use our L'hopital's rule calculator to solve the Limits for undefined functions (0/0, ∞/∞).
Frequently Asked Questions- FAQ’s
What is the concept of a limits calculator?
A limits calculator is an online tool that calculates the limit of a provided mathematical function as the input value approaches a particular value or infinity (in some cases).
Why do we use limits in math?
A limit, a mathematical concept based on the idea of approximation, is mainly used to assign values to some functions at points where the values are not defined, so that it matches nearby values.
Why are limits important in Calc?
A limit tells us the value the function will approach when the inputs to the function approach a certain number. The concept of a limit is absolutely fundamental to both differential and integral calculus.
References
- Wikimedia Foundation. What are Limits? Wikipedia.
- OpenStaxCollege. (2016, February 1). Rules of Limits. 2.3 The Limit Laws | Calculus Volume 1.



