To calculate result you have to disable your ad blocker first.
Calculadora de continuidad
Ingrese la función, seleccione la variable, ingrese el punto y presione calcular Botón para evaluar la continuidad de la función usando la calculadora de continuidad.
Table of Contents:
Calculadora de continuidad
La calculadora de continuidad determina si la función es continua o discontinua. Esta calculadora continua encuentra el resultado con pasos en un par de segundos.
¿Qué es la continuidad?
En cálculo, continuidad es un término utilizado para comprobar si la función es continua o no en el intervalo dado. El continuidad Se puede definir como si la gráfica de una función no tuviera ningún agujero o rotura. Si hay un agujero o una interrupción en el gráfico, entonces debería ser discontinuo.
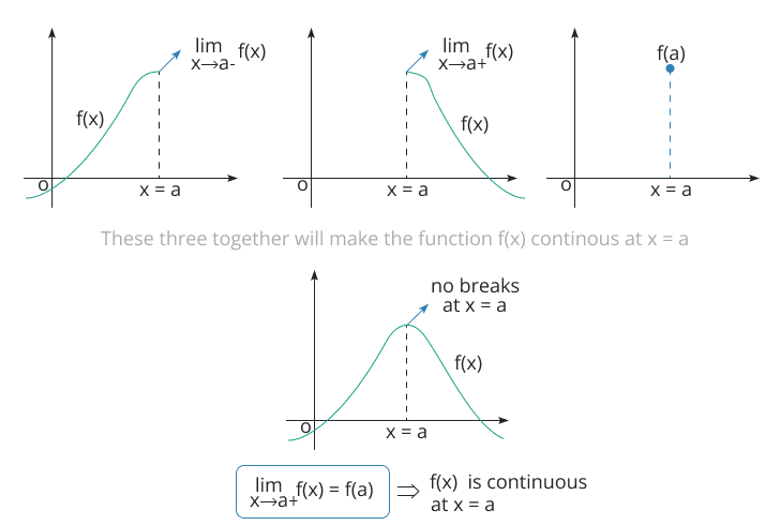
El concepto de continuidad es muy esencial en el cálculo ya que diferencial solo es aplicable cuando la función es continua en un punto. Si la función no es continua, entonces no es posible la diferenciación.
Matemáticamente, un la función debe ser continua en un punto x = a si satisface las siguientes condiciones.
- fa) existe (la función debe definirse en " a ”)
- Lim x→a f(x) existe (límite de la función en “ a " debe existir)
- f(a) = limx→a f(x)
Si se cumplen las tres condiciones, entonces la función es continua; de lo contrario, es discontinua.
¿Cómo calcular la continuidad?
A continuación se muestra un ejemplo resuelto de continuidad para aprender a calcularla manualmente.
Ejemplo 1
Comprobar si una función dada es continua o no en x = 2 .
f(x) = 3x 2 + 4x + 5
Solución
Paso 1: Compruebe si la función está definida o no en x = 2 .
f(2) = 3(2) 2 + 4(2) + 5
= 3(4) + 4(2) + 5
= 12 + 8 + 5
= 25
Por lo tanto, la función se define en x = 2 .
Paso 2: Evaluar el límite de la función dada.
Lim x>2 [3x 2 + 4x + 5] = límite x>2 [3x 2 ] + lím x>2 [4x] + lím x>2 [5]
= 3lim x>2 [X 2 ] + 4lim x>2 [x] + lím x>2 [5]
= 3[22] + 4[2] + [5]
= 3(4) + 4(2) + 5
= 12 + 8 + 5
= 25
Por tanto, el límite de la función existe.
Paso 3: Verifique la tercera condición de continuidad.
f(2) = limx→2 f(x)
25 = 25
Por tanto la función es continuo ya que se cumplen todas las condiciones.
Ejemplo 2:
Verifique si una función determinada es continua o no en x = 0 .
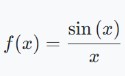
Solución
Paso 1: Compruebe si la función está definida o no en x = 0 Luego luego
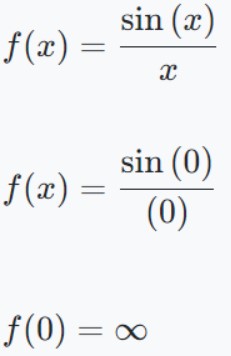
Por lo tanto, la función no está definida en x = 0 .
Paso 2: Calcula el límite de la función dada.
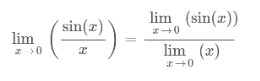
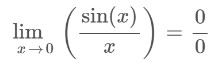
Como la función da formato 0/0, aplique La regla de L'hopital de límite para evaluar el resultado.
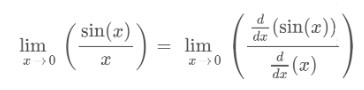
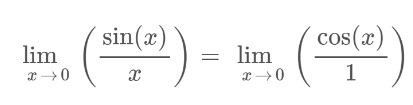
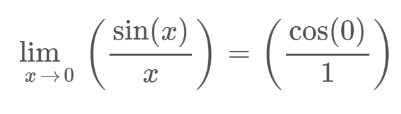
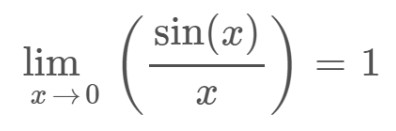
Paso 3: Verifique la tercera condición de continuidad.
f(0) = límite x>0 F (x)
& finalmente = 1
Condición 1 &erio; 3 no está satisfecho. Entonces, la función es discontinuo .

