Introduction to Arithmetic Sequence, Nth Term and Common Difference

Sequences are ordered lists of numbers. They always have a definite pattern. This pattern makes it easy to predict or calculate the next value in the sequence.

Some examples of sequences are:

• 2, 4, 6, 8, …
• 3, 9, 81, 6561.
• 18, 16, 14, 12, ...

It can be seen that the rest of the values are predictable if we know only the first 2 or 3 values. Sequences are both finite and infinite. 

There are different formulas of sequences that help to find the nth term. Since sequences have different types so the formulas used are also different e.g arithmetic sequences, geometric sequences, e.t.c.

You will learn what is an arithmetic sequence, what are the nth term and common differences with exmaples and their solutions. 

What is Arithmetic sequence?

An arithmetic sequence is one of the many types of sequences. It is by far the easiest to understand and calculate.

Definition

An arithmetic sequence is:

“A sequence in which the next value is the sum of the preceding number.”

In simple words, if ‘A1’ is the first term then ‘A2’ is calculated by adding a constant ‘b’ to ‘A1’. Similarly, ‘A3’ is calculated by adding the same constant to ‘A2’.  

The arithmetic sequence is also known as Arithmetic progression. Some examples of an arithmetic sequence are:

• 0, 4, 8, 12, 16, …
• 1, 2, 3, 4, 5.
• 10, 8, 6, 4, ...

Common Difference

The constant ‘b’ discussed above is a common difference. It is such a number, when added to the previous term, gives the next term of the sequence.

It is denoted by d. It can be both positive or negative integer. In the examples given above, the common differences can be found after a subtracting the next term from the previous one.

In the first example, 0, 4, 8, 12, 16, …

the common difference is 4.

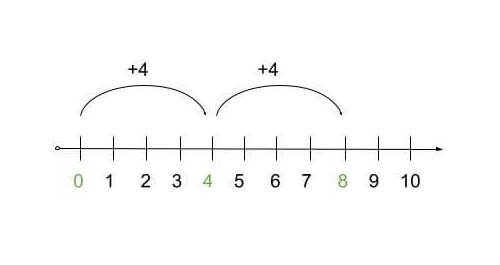
We can see that when four is added to 0, the next term is 4. Moving on, when 4 is added to 4, the next term is 8, and so on.

Common Difference Formula

You can also use a formula to find d. 

d =  a_n -  a_n-1

First-term:

First-term is the term at the very start of the sequence. It is most commonly represented by a₁. In the sequence below, the first term is 0.

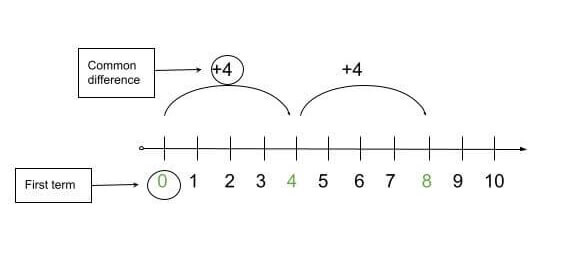
Nth term:

The letter ‘N’ represents the term position or general term. It means the nth term could be any number of the sequence. It can be 5th, 10th, or even 100th. 

It totally depends on which term you want to know. It is represented by a_n.

Arithmetic Sequence Formula

As we know that 

• The first term is a
• The second term is (a + d)
• The third term is (a + 2d) and so on 

To find the arithmetic sequence, use the below formula:

a + (a + d) + (a + 2d) + … 

As you have read before, there is a special formula that helps to find the nth term of every sequence. This formula for an arithmetic sequence is 

Nth Term Formula

a_n  =  a_n-1 + d

To calculate nth term through first term and d, the formula is 

a_n  =  a₁ + (n - 1) d

In this equation:

• a_n is the nth term
• a₁ Is the first term
• d is the common difference.

You can use the arithmetic sequence calculator as well to find arithmetic sequence as wel as nth term.

Sum of Arithmetic Sequence (Progression) Formula

S = n/2 × [2a₁ + (n - 1)d]

Arithmetic Sequence Examples and Practical Problems

Now that you have been introduced to arithmetic sequence and have learned its formula for the nth term. It is time to use this formula in examples.

Nth Term - Examples

Problem # 1: 

An arithmetic sequence is 1, 7, 13, 19, …

Find the 8th term of this sequence.

Solution:

Step 1: Identify the terms.

First-term = 1

Nth term = 8th

The common difference is   = (2nd term - 1st term) = 7 - 1 = 6

Step 2: Use the nth term formula and place the values in it.

a_n =  a₁ + (n - 1) d    

a_n = 1 + (n - 1) 6

= 1 + 6n - 6

=  6n - 5

Step 3: Find the nth term by simplifying.

a₈ =  6n -  5

=  6(8) - 5

a₈ =  43

Problem # 2:

The 13th term of a sequence is 89. The common difference is 5. For this data, find 

1. The first term of the sequence.
2. Find the 17th term and 5th term

Solution:

We know that 13th term is 89 and the common difference is 5.

a_n = 89, d = 5

Finding first term:

Step 1: Put thevalues in the formula.

a_n  =  a₁ + (n - 1) d 

89 =  a₁ + (17 - 1) 5  

89 =  a₁ + 80

 a₁ = 89 - 80

 a₁ = 9 

Finding 5th and 17th term of the sequence:

Step 2: Use the nth term formula.

a_n =  a1 + (n - 1) d    

a_n = 9 + (n - 1) 5

=  9 + 5n - 5

a_n =  5n + 4

Step 3: Find the 17th term.

a₁₇ = 5n +  4

= 5 (17) + 4 

a₁₇ = 89

Step 4: Find the 5th term.

a₅ = 5n +  4

= 5 (5) + 4 

a₅ = 29

Problem # 3:

For the given data, find the general terms of the arithmetic sequence.

  a₁₁ = -13

  a₉  =  -9

Solution:

We will find linear equations of these terms and perform the elimination method to find the required values.

Step 1: Put the values of the 9th and 11th terms in above equations.

a₉ =  a₁ + (9 - 1) d

-9 =  a1 + (9 - 1) d 

-9 =  a1 + 9d - d

- a1 = 8d + 9   eq (i)

a₁₁ =  a₁ + (11 - 1) d 

-13 =  a1 + (11 - 1) d

-13 =  a1 + 11d - d

- a1 =  10d + 13   eq (ii)

Step 2: Subtract eq (ii) from eq (i).

-   a₁ =  10d + 13 

-(- a₁ =   8d + 9)

 _________________

       = 2d + 4

-4 = 2d

d = -2

Step 3: Place the value of d in eq (ii).

a₁ = - 8(-2) - 9  

= 16 - 9 = 7

Hence the general term is calculated by 

a_n =  a₁ + (n - 1) d    

a_n =  7 + (n - 1) (-2)    

a_n = -2n + 5

Arithmetic Sequence - Examples

Problem # 4:

Find the arithmetic sequence upto 6th term if 

 a₁ = 5

 d  = -3

Solution:

The formula is: a, (a + d), (a + 2d) + …

Now, 

a₁ = a = 5

a₂ = a + d= 5 + (-3) = 2

a₃ = a + 2d = 5 + 2(-3) = -1

a₄ = a + 3d = 5 + 3(-3) = -4

a₅ = a + 4d = 5 + 4(-3) = -7

a₆ = a + 5d = 5 + 5(-3) = -10