To calculate result you have to disable your ad blocker first.
Slope Intercept Form: How to find Equation of Straight Line with two Points

Publish Date: 08 Aug, 2023
Table of Content

As you may already know, linear equations can be represented in several ways. For example, if we have an equation y = 3x - 6, we can represent it as
- y - 3x = -6
- y = 3(x - 2)
- (y + 6) / 3 = x
And many more ways. But there is one way of writing a linear equation that is most common and useful. This way is called the Slope-Intercept Form.
It is the most popular one and you can easily get more than half of the information about a linear equation by just looking at it.
So without further delay, let’s learn what is the slope-intercept form and how it can help us to find a linear equation from two points.
What is Slope Intercept Form?
You might be wondering why we need to find a linear equation if we already have a slope-intercept form (even if you don’t know about it yet).
It’s because the slope-intercept form is a general equation. It is used to find specific linear equations. It is a structure on which linear equations are found.
The equation of the slope-intercept form is
Y = mx + b
Constant values
Looking at this equation, all you see are alphabets. But one can identify the most commonly used variables ‘x’ and ‘y’. While the alphabets ‘m’ and ‘b’ represent constant values.
What do constant values tell us?
The constants of this equation represent:
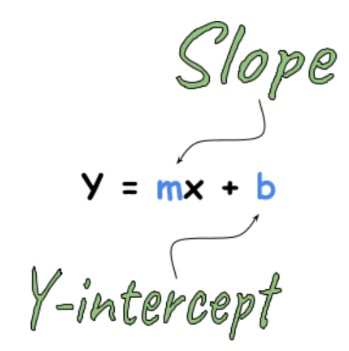
Constant value b:
This value represents the y-intercept of the equation. The y-intercept is the point in the cartesian plane where the line meets the x-axis.
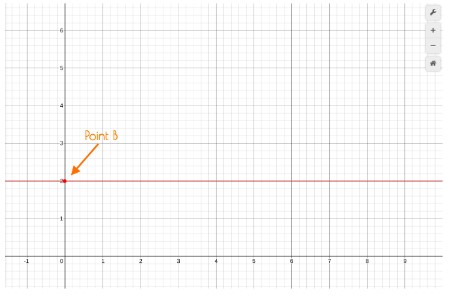
This statement can be proved. If we put x=0 in the equation because at the y-axis, x is zero. We will get:
Y = mx + b
Y = m(0) + b
Y = b
Constant value m:
This value represents the slope of the equation. The slope of a line is defined as “rise over run”, where the rise is the value along the y-axis and run is the value along the x-axis.
The slope formula is:
Slope = change in y / change in x
= y2 - y1 / x2 - x1
= Δy / Δx
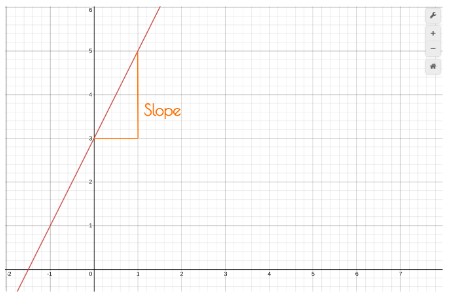
This can also be proved. We know that when the value of x increases by one, the value of y increases by the value of the slope i.e
Slope = change in y / 1
From previous calculations, we know when x = 0 then y =b. This makes a point (0,b). Now, if we put 1 in the place of x in the equation, what will be y?
Y = m (1) + b
Y = m + b
So, we have two points (0, b) and (1, m+b). Let’s find the slope between these points.
Slope = change in y / change in x = y2 - y1 / x2 - x1
= m+b - b / 1 - 0
= m/1 = m
Hence, proved that m represents the slope of the linear equation in the slope-intercept form.
Now, we will see this with an example. We have an equation:
Y = -x + 2
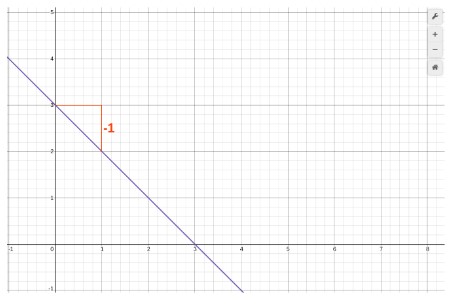
Using our previous knowledge, we can identify the value of slope i.e. -1. But let’s prove it by increasing the value of x by 1 for every step and see the changes.
Y = -x + 2
For x = 0, Y = (-1)(0) + 2 = 2
For x = 1, Y = (-1)(1) + 2 = 1
For x = 2, Y = (-1)(2) + 2 = 0
For x = 3, Y = (-1)(3) + 2 = -1
One can see that at every step, the value of ‘y’ decreased by -1.
Equation of line with two points
Here we will see how we can form a linear equation of slope-intercept form with two points.
Say we have two points (0,6) and (2,0). If we were to make a linear equation from these points, how would we do that?
Before that, look at the graph of these points.
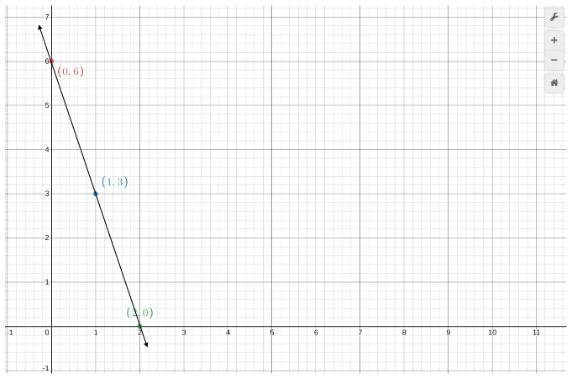
Looking at this graph, can you identify the y-intercept? If you thought it’s (0,6), then you were right. That means we already have the value of b and that is 6.
For slope, we will use the formula:
Slope = change in y / change in x = y2 - y1 / x2 - x1
m = (0 - 6) / (2 - 0)
m = -6 / 2
m = -3
This value represents that for every increase of 1 in x, y will decrease (due to the -ve sign) by 3.
Let’s use these values in the general structure of the slope-intercept equation to find a linear equation for these points.
Y = mx + b
Y = (-3)x + 6
This can also be written as:
Y = 6 - 3x
Now you know how to find a linear equation from two points. Let’s use this knowledge to solve some problems.
Examples - Finding Equation of Straight Line
Using slope and y-intercept:
If a straight line has a slope of -1 and its y-intercept is 3. Find the linear equation.
Solution:
Step 1: Identify the given information.
m = -1
b = 3
Step 2: Put in the equation.
Y = mx + b
Y = (-1)x + 3
Y = 3 - x
Using one point and slope
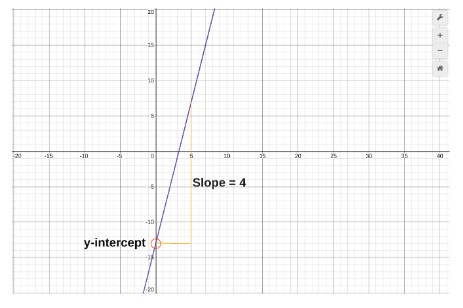
What is the slope-intercept form of a straight line if;
Slope = 4
Point = (5,7)
Solution:
Step 1: Find b by putting the point in the general form.
Y = mx + b
7 = (4)(5) +b
7 = 20 + b
b = -13
Step 2: Make the equation.
Y = mx + b
Y = 4x - 13
Using two points
Two points (2,3) and (7,8) are on a cartesian plane. Use these points to give a linear equation.
Solution:
These points on a graph look like this:
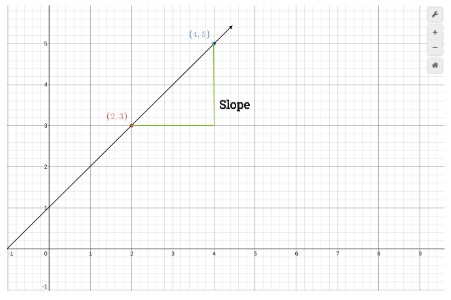
Step 1: Calculate the slope.
Slope = Δy / Δx = (4-2) / (5-3)
= 2 / 2 = 1
Step 2: Find b.
As we know, in the slope-intercept form b means y-intercept. So if we use the formula;
y = mx + b
Using point 1 i.e (2,3):
3 = (1)(2) + b
3 - 2 = b
b = 1
Step 3: Form the equation.
b = 1
m = 1
The equation will be;
Y = (1)x + (1)
Y = x + 1
You can verify all these calculations using Slope intercept form calculator.
🖩Related Tools
📝Recent Blogs

