To calculate result you have to disable your ad blocker first.
Introduction to Integrals: Definition, Rules, Examples, and Solution

Publish Date: 08 Aug, 2023
Table of Content
We can find the area under a straight line on a graph through different formulas. But have you ever wondered how to find the area under a curve line? Because if yes, no worries, we are on the same page.
We already know that we can calculate the slope of a curve line through differentiation. Now, let’s try to figure out the formula for the area under a curve line.
For better understanding, consider this graph.
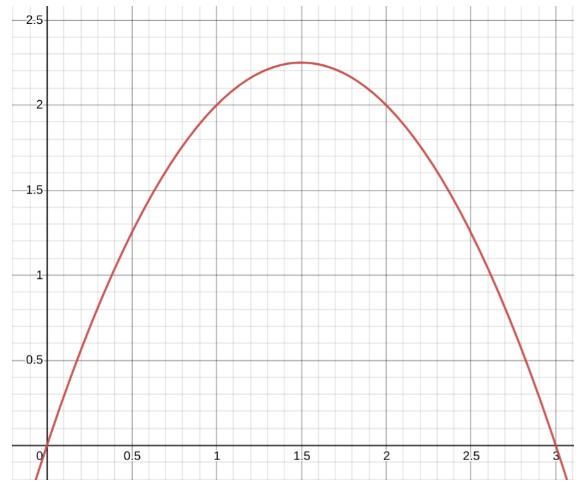
How can the area under the curve from point 0 to 3 on and above the x-axis be calculated?
According to Riemann, the sum of the area of definite rectangles under the curve line gives the approximate area under that curve. Something like this:
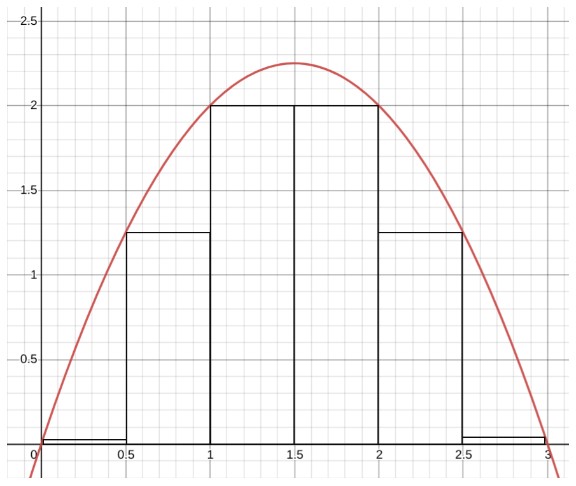
But this is not satisfying enough. How about we decrease the width of rectangular slabs. And some more and some more. Maybe like this:
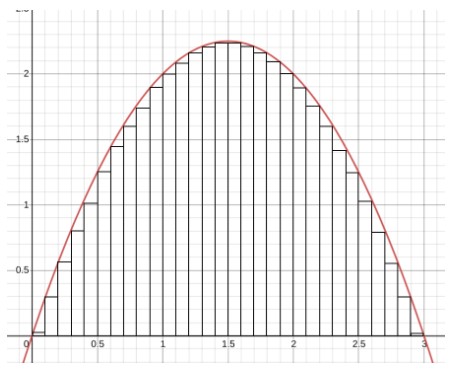
This area will be relatively more accurate than the previous one. But what if...we decrease it some more. So much that it's almost zero! Did something click in your mind?
YES, Derivatives! Derivatives are used to calculate instantaneous slope. We are going to use that concept to find the area under this curve. This concept is called integrals.
Let’s learn what integrals are? What are the rules of integrals and how to solve them?
What are Integrals?
Integration is the process of finding integrals. Integrals have many applications such as for finding volumes, mass e.t.c But in this article, we will discuss the area under a curve.
Definition of integral is:
“If the derivative of a function is f’(x) then its integral is ∫f(x).dx + c.”
This can be explained with an example. Consider a function and Its derivative i.e f’(x) = 3. But what is its antiderivative? We can make some assumptions.
If you think, we get a constant term as a derivative for a function with a single X. That is:
= 3x
So, we get the original function 3x by antidifferentiation.
Integration Coefficient
Look at these equations:
- 3x + 12
- 3x + 100
The derivative of all these equations is also 3x. So to clear any mistake, we write:
= 3x + C where c could be any constant number
This is why integral has all the possible antiderivatives of that function.
Now that you know what is integral, we will now learn integral notation.
Integral Notation
Every operation has its operator, a symbol. For derivatives, we have d/dx notation. Similarly, for integrals, we use a fancy s.
∫ fx.dx + c
Integrals vs Derivatives
You might wonder “I now know what is integral but how is it related to derivatives?”.
To be precise, Antiderivatives (reverse differentiation) and indefinite integrals are almost the same things. But there is a big difference between definite integrals and antiderivatives.
When we find the derivatives, we lower the difference between the two points so much that it is infinitesimally small. But in integrals, we make so many small parts that the number of these reaches infinity.
In simple words, in derivatives, we apply the limit of approximately zero value and in integration, we apply the limit to infinity. So, we can say that integrals are inverse derivatives.
Rules of Integrals
There are some rules that help to solve integrals in the same way we use rules of differentiation. Rules of integrals are quite related to the rules we use to solve derivatives.
Power Rule
When a function is raised to some power then the rule used for integration is:
∫ fx.dx = (xn+1)/n+1
It is derived from the power rule of differentiation. Let’s first prove that this rule is the reverse of the power rule for differentiation.
Example
The derivative of a function is 6x2. Let’s revise the process of differentiation and do the opposite of it.
- One is subtracted from the power of a function, so to find its inverse we add one in the power i.e 6x2+1 = 6x3.
- The coefficient is the same as the power so to reverse it we will divide by the same number i.e 6x3/3 = 2x3.
So the integral of 6x2 is 2x3 (the original function). To verify if the derivative of 2x3 is 6x2, use the derivative calculator.
Multiplied with constant
When we see a function that is in multiplication with some constant number, we apply a rule. According to this rule, during integration, the constant term is taken out of the integral notation.
∫k.fx dx =ck ∫fx dx
Example
A function is f(y) = 6y2 + 12y. You can see the constant numbers 6 and 12. Let’s take 6 common.
= 6 ( y2 + 2y)
Apply integration:
∫ 6y2 + 12y .dy = 6 ∫ y2 + 2y .dy
Applying power rule:
= 6 ∫ y2 + 2y .dy
= 6 { (y2+1)/2+1 + 2y1+1/1+1 }
= 6 { y3/3 + y2}
= 2y3 + 6y2 + c
Sum Rule
When two functions are in addition then on integration they can be integrated separately and then added afterward.
∫ (fx + gx).dx = ∫ fx.dx + ∫ gx.dx
Example
Find the integral of u5 + 2u.
Solution:
∫u5 + 2u.du = ∫u5.du + ∫2u.du
= (u5+1/ 5+1) + 2∫u.du
= u6/6 + 2u1+1/2
= u6/6 + u2 + c
Difference Rule
Similar to the sum rule, when functions are in subtraction, they can be integrated separately.
∫ (fx - gx).dx = ∫ fx.dx - ∫ gx.dx
Example
Find the integral of u5 - 2u.
Solution:
∫u5 + 2u.du = ∫u5.du - ∫2u.du
= (u5+1/ 5+1) - 2∫1u.du
= u6/6 - 2u1+1/2
= u6/6 - u2 + c
You can see from the example above, the only difference between the sum and difference rule is the sign symbol.
Integration by Parts
It is the inverse of the product rule of differentiation. Let’s derive its formula.
The product rule is:
(uv)’ = uv’ + u’v
Apply integration on both sides.
∫(uv)’.dx = ∫ uv’.dx + ∫ u’v.dx
uv = ∫ uv’.dx + ∫ u’v.dx
∫ uv’.dx = uv - ∫ u’v.dx
Example
Evaluate ∫ x.cosx .dx
Solution:
Identify u and v’.
u = x
v’ = cosx

Find the values of u’ and v.
For u’, find the derivative of u.
u = x
u’ = 1
For v, find the integral of v’.
v = cosx
∫v.dx = ∫ cosx.dx = sinx
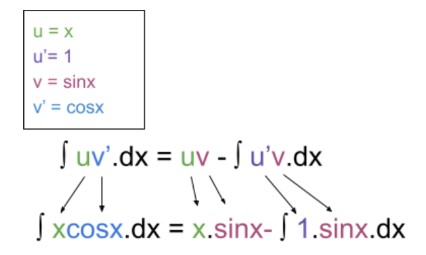
Solve.
∫xcosx.dx = x.sinx - ∫1.sinx.dx
= x.sinx - cosx
Add constant.
= x.sinx - cosx + c
Substitution Rule
This rule is also known as the reverse chain rule. This rule is applied in special situations. Sometimes the function can be set up in a way where the substitution rule can be applied.
The rule is:
∫ f((gx)).g’(x).dx = ∫f(u).du
To understand this formula look at the operations involved.
g’(x) = d/dx g(x)
For convenience, let
u = g(x) then du = g’(x)
It is to be noted that this formula is only applicable when there are both u and u’ in the function to be integrated.
Example
Find the integral of (x + 1)2.
Solution:
Understanding the function we can see that the derivative of x + 1 is 1. This means we can multiply 1 to use the substitution rule.
∫(x + 1)2.dx = ∫(x + 1)2.1dx
We now have u and u’ that are x + 1 and 1 respectively. Using the formula:
∫(x + 1)2.1dx = ∫ u2. du
= ∫ u2+1 / 3
= ∫u3/3
Putting back the value of u:
= ∫(x+3)3 / 3
Some other Rules
Function | Integral |
∫cos(x).dx | sinx + c |
∫sin(x).dx | -cosx + c |
∫sec2(x).dx | tanx + c |
∫(1/x).dx | ln|x| + c |
∫ex . dx | ex + c |
∫ln(x).dx | x ln(x) - x + c |
Types of Integrals: Indefinite and Definite Integrals
There are two types of integrals. Both are solved differently and have different applications.
Indefinite Integrals
It is the reverse of a derivative. It calculates the whole area under a curve line graph. All of the examples that you have seen in this article so far are of indefinite integration.
In these integrals, lower and upper bound limits are not applied. Moreover, a constant c is added in the end to indicate that the answer includes all the possible antiderivatives of the function.
Let’s take an example of a pool. Consider that you are filling the pool up with the help of a water pipe. The water flow is changing now and then due to some reason.
Now if the flow rate was consistent, it would have been easy to calculate the volume of water in the pool after some time t.
But the problem is that the flow rate is constantly changing and cannot be measured at just one point. It is necessary to find the flow rate at every point to know the exact volume.
For this purpose, we use indefinite integrals. Flow Rate is calculated by derivatives and it tells at which rate the pool is filling up at the time t.
d/d (x2) = 2x (flow rate)
The integration tells that what is the volume of the water in the pool after time t.
∫2x.dx = x2 (volume)
This also confirms the fact that integrals are antiderivatives.
Now, what if there was already some water c in the pool? This means our calculated volume is not the “the net volume”. To get the right answer, add c in the answer.
= x2 + c
Definite Integrals
Definite integral finds the volume under a specific time interval. For example, you want to calculate the volume accumulated between points a and b on the x-axis.
To calculate the area between 1 to 3 on the x-axis, we apply the upper and lower bound limits. This way, you will find the exact definite area of the highlighted portion.
Continuing the example of the pool, let’s assume we want to find the volume of water added to the pool between the minute 5 and 8. We will write:
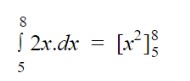
After integrating the function put the values of a and b respectively and subtract the b value from the a value.
= [(8)2 - (5)2]
= 64 - 25
= 39
The antiderivative calculator can find both definite and indefinite integrals for a given function.
Wrapping Up
Integrals are used to find the area under a curve. It is represented by the stylish S symbol. Integral rules help in the process of integration. Integrals can be definite or indefinite (antiderivatives).
🖩Related Tools
📝Recent Blogs

