Triangle Circumcenter calculator

The circumcenter of a triangle calculator is used to find the point which is concurrent for all three bisectors of the triangle.

What is the circumference of a triangle?

It is the point where the three lines bisecting the sides of the triangle meet. These lines divide the sides of the triangle into two equal parts. 

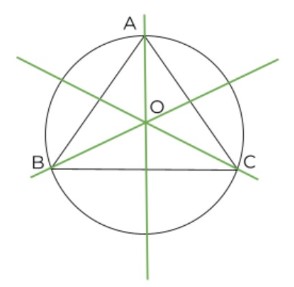
This point can be inside (for acute triangle) as well as outside (for obtuse triangle) of the triangle. 

How to find the circumcenter of the triangle?

There is a whole process you need to follow to find the circumcenter of the triangle.

1. First, you need to find the midpoint of the three sides of the triangle.
2. Now find the slope of the perpendicular bisector to all these lines. 
3. Make the point-slope equation of the sides. y - y₁ = m(x - x₁) 
4. Solve any two of the equations to find the point of intersection. This point is the circumcenter.

The triangle circumcenter uses the same process therefore the results are accurate.

Example:

Find the circumcenter of the following triangle.

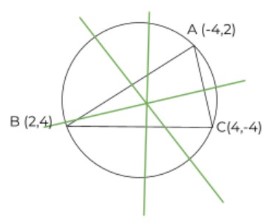
Solution:

Step 1: Write all the points.

A = (-4,2)

B = (2,4)

C = (4,-4)

Step 2: Find the midpoint using its formula.

The formula of the midpoint is:

Midpoint = (x₁ + x₂) / 2 , (y₁ + y₂)/2

AB = (-4+2)/2 , (2+4)/2 

= -2/2 , 6/2

= -1 , 3

BC = (2+4)/2 , (4-4)/2 

= 6/2 , 0

= 3 , 0

CA = (4-4)/2 , (-4+2)/2 

= 0/2 , -2/2

= 0 , -1

Step 3: Calculate the slope of the lines.

AB = (4 - 2) / (2 + 4) 

= 2 / 6

= 1/3

Slope of AB perpendicular = -1/(1/3)

= -3

BC = (4 + 4) / (2 - 4)

= 8 / -2

= -4

Slope of BC perpendicular = -1/(4)

= 1/4

CA = (2 + 4) / (-4 - 4)

= 6 / 0

Slope of CA perpendicular = -1/(0)

= 0

Step 4: Make point-slope equations for any two points.

The values of x₁ and y₁ are from the midpoint values.

For AB; m = -3, x₁ = -1, and y₁ = 3

y - y₁ = m ( x - x₁ )

y - 3 = (-3)(x + 1)

y = -3x - 3 + 3

y = -3x … equation 1

For BC, m = ¼, x₁ = 3, and y₁ = 0

y - y1 = m ( x - x₁ )

y - 0 = (1/4)(x - 3)

y = 1/4x -3/4

4y = x - 3 … equation 2

Step 5: Find the value of x by putting the value of y in equation 2.

4y = x - 3

4(-3x) = x - 3

-12x = x - 3

-13x = 3

X = -3/13

Step 6: Use the value of x to find the y.

Y = -3(-3/13)

Y = 9/13

Circumcenter = (-3/13 , 9/13) 

As you can see the process is quite lengthy. The best alternative to save time is to use the circumcenter solver.