To calculate result you have to disable your ad blocker first.
Gauss Jordan Calculadora
Seleccione el orden de la matriz, complete los cuadros de entrada requeridos y haga clic en el botón calcular usando la calculadora de eliminación gaussiana
Calculadora Gauss Jordan
La calculadora de eliminación gaussiana reduce una matriz formada por un sistema de ecuaciones a su forma simplificada. Encuentre otra información y valores relacionados con la matriz como:
- Matriz inversa
- Determinante
- Valores propios
- Propiedades, traza, etc.
Dado que esta herramienta resuelve aún más la eliminación gaussiana, también se la conoce como calculadora Gauss-Jordan.
¿Qué es la eliminación gaussiana?
Este método lleva el nombre de Carl Freidrich Gauss. Utiliza el método escalonado por filas para alcanzar la forma matricial deseada. Luego, los valores de las variables de la ecuación matemática se calculan fácilmente a partir de la matriz resultante.
Utiliza una matriz aumentada.
¿Cómo realizar la eliminación gaussiana?
Las operaciones de fila se utilizan en una matriz para hacer que las entradas diagonales sean 1 con ceros debajo. Además, se utiliza para convertir la matriz en una matriz diagonal. De esta forma los valores se reconocen a partir de la propia matriz reducida.
En primer lugar, debe organizar la ecuación de tal manera que todas las mismas variables se alineen con el tornillo de banco de la columna. Si una de las ecuaciones no contiene ninguna variable, entonces coloque 0 en su lugar en la matriz.
Veamos un ejemplo utilizando este método.
Ejemplo:
Encuentre los valores de las variables utilizadas en las siguientes ecuaciones mediante el método de eliminación de Gauss-Jordan.
1x + 1y + 2z = 9
2x + 4y - 3z = 1
3x + 6y - 5z = 0
Solución:
Paso 1: Reorganiza las ecuaciones para hacerlas iguales a 0.
3x + 8y - 7 = 0
6x + 3y - 3 = 0
9x + 4y - 4 = 0
Paso 2: Haz una matriz aumentada.
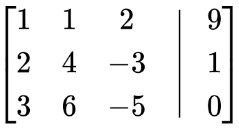
Paso 3: Realizar reducción escalonada por hileras.
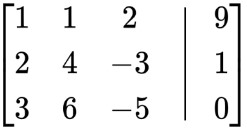
Resta la fila 1 multiplicada por 2 de la fila 2: R 2 =R 2 -2R 1
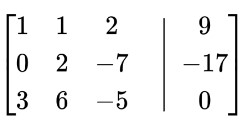
Sustraer fila 1 multiplicada por 3 de la fila 3: R 3 =R 3 -3R 1 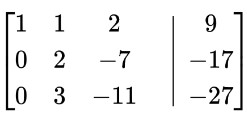
Divida la fila 1 por 2: R 2 =R 2 /2 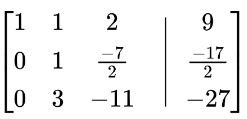
Resta la fila 2 multiplicada por 3 de la fila 3: R 3 =R 3 -3R 2
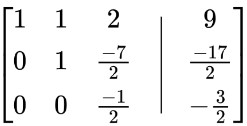
Multiplicar fila 3 por -2: R 3 = -2R 3
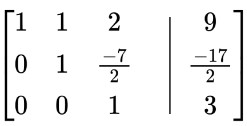
Este es el final del método de eliminación gaussiano. Los valores de las variables se pueden calcular fácilmente a partir de esta matriz. La primera columna representa x, la segunda es para y y la tercera muestra la variable z.
Sólo hay z en la tercera fila. Eso significa z=3. Coloque esto en la segunda fila para calcular y y luego en la primera fila para encontrar x.
Esta matriz se puede simplificar aún más utilizando el método de Gauss-Jordan. Para eso:
Agregar fila 3 multiplicada por 7/3 a fila 2: 7/3R 3 +R 2 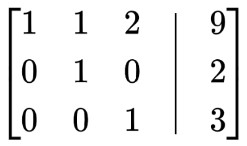
Resta la fila 3 multiplicada por -2 de la fila 1: R 1 =R 1 -2R 3 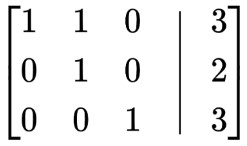
Resta la fila 2 de la fila 1: R 1 =R 1 - R2 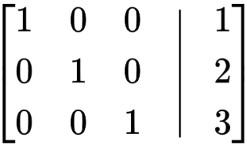
A partir de esta matriz, encontrar el valor de las variables es sólo cuestión de mirar. z=3, y=2 yx=1.

