What is Adjacent Angle? Explained with its Properties and Applications

The concept of adjacent angles has been a fundamental part of geometry and mathematics for centuries. Babylonians developed an early system of measurement and geometric principles.

With the advancement of mathematical knowledge and the introduction of new branches of geometry, such as non-Euclidean geometries in the 19th century, the study of angles expanded further. However, the concept of adjacent angles remained an essential element in geometry education and problem-solving.

While the concept of adjacent angles itself hasn’t significantly evolved, its understating and application have been refined through the contributions of countless mathematicians and educators throughout history.

In this article, we will discuss the basic concept of adjacent angles and their properties and solve examples for better understanding.

What is an Adjacent Angle?

“Adjacent corners are corners that have a common vertex and do not intersect.”

In other words, they are angles that are next to each other, sharing a common endpoint and a common side. The common side is usually a ray or a line segment. The angles can be formed by intersecting lines or by the sides of a polygon.

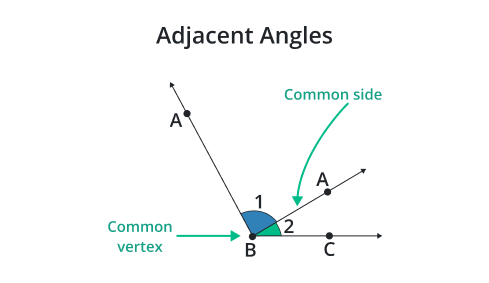
Understanding adjacent angles is important in geometry as it helps analyze and solve problems involving angles, lines, and polygons.

Adjacent Angle’s Properties:

Here are some properties of adjacent angles:

• Common vertex
• Common side
• Non-overlapping
• Sum of measures
• Linear pair
• Exterior angles

Common vertex:

Adjacent corners have a common vertex, where the two corners meet.

Common side:

Adjacent angles also share a common side, which is a line segment that forms a part of both angles.

Non-overlapping:

They are distinct and separate angles. Adjacent angles do not overlap or intersect each other.

The sum of measures:

The sum of the measures of adjacent angles is equal to the measure of the larger angle formed by their outer arms.

Exterior angles:

The exterior angle is formed by one of the arms of an adjacent angle and the extension of the other arms of an adjacent angle and the extension of the other arm complements the adjacent angle.

Applications of adjacent angles:

Adjacent angles have several applications in various fields, here are some examples:

• Trigonometry
• Engineering and Architecture
• Surveying and mapping
• Computer graphics and animation:
• Robotics and automation
• Game development
• Navigation and GPS
• Art and design

Trigonometry:

Adjacent angles are essential in trigonometry, which deals with the relationships between the angles and the sides of a triangle.

Engineering and Architecture:

Engineers and architects use the concept to ensure proper alignment and stability of beams, columns, and other building components. Adjacent angles play a crucial role in the design of structures.

Surveying and Mapping:

By measuring angles between landmarks or using theodolites, they can create precise maps and boundaries.

Computer and Graphics and Animation:

Objects can be rotated, transformed, and animated by manipulating angles in virtual environments.

Robotics and Automation:

In robotics, adjacent angles are utilized in joint movements of robotic arms and mechanisms.

Game Development:

Adjacent angles are employed in game development for simulating realistic physics and movements.

Navigation and GPS:

The angles between satellites and receivers help determine the location accurately.

Art and Design:

Artists and designers consider adjacent angles when composing visual elements. By understanding the relationships between angles, they create balance, harmony, and dynamic compositions in paintings, sculptures, and other forms of visual art.

Examples of Adjacent Angles:

Example 1:

Find all the pairs of adjacent angles.

Solution:

Here we can observe that the list of adjacent angles is the following:

1. ∠AOE, ∠EOC
2. ∠EOC, ∠COB

iii.        ∠COB, ∠BOD

1. ∠BOD, ∠AOD
2. ∠AOD, ∠AOE

Example 2:

If ∠AOB = 130^o, and ∠AOC = 80^o then find the value of x in adjacent angles.

Solution:

Step 1: Extract data

∠AOB = 130^o

∠AOC = 80^o

∠COB = x

Step 2: find the value of x

∠AOB = ∠AOC + ∠COB

130^o = 80^o + x

x = 130^o – 80^o

x = 50^o