Triangular Numbers: Definition, Formula, Properties, & Examples

Triangular numbers are a sequence of numbers that can be visualized as the number of dots in an equilateral triangle arrangement. They are a subset of figurate numbers, which are numbers that represent regular geometric shapes using dots.

Triangular numbers hold a unique place in mathematics due to their elegant geometric representation and various interesting properties. In this article, we'll define its definition, the formula to calculate, properties, and applications.

What are Triangular Numbers?

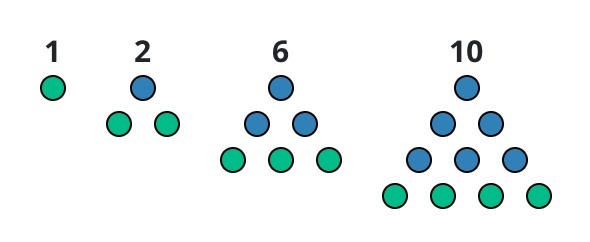
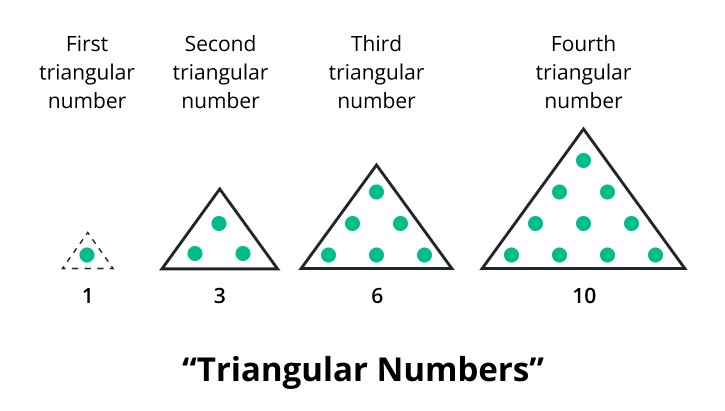
Triangular numbers are a sequence of natural numbers that can be represented in the form of equilateral triangles. Imagine arranging dots in the shape of a triangle, starting with just one dot at the apex. The number of dots increases by one with each additional row.

The total number of dots in each triangular arrangement corresponds to a triangular number.

Triangular Number Formula

Calculating triangular numbers can be simplified using a formula. Let’s denote T_n as the n^th triangular number. The formula to find the value of T_n is:

Tn = n × (n + 1) / 2

Here,

• “n” represents the position of the triangular number in the sequence.

The sum of Triangular Numbers:

The sum of a sequence of triangular numbers can be calculated using a formula that involves the triangular number itself. If you are summing up the first “n” triangular numbers, the formula is:

Sum = T1 + T2 + T3 + ... + Tn = n × (n + 1) × (n + 2) / 6

Here,

• “T_k” represents the kth triangular number in the sequence.

This formula provides a convenient way to find the sum without having to manually calculate each triangular number and then add them up.

Properties of Triangular Numbers:

Triangular numbers possess several properties some noteworthy include:

• Sum of Consecutive Numbers: Each triangular number is the sum of the first “n” natural numbers.
• Difference of Consecutive Triangular Numbers: The difference between consecutive triangular numbers is always a natural number.
• Connection to Square Numbers: The sum of any two consecutive triangular numbers is a perfect square.
• Geometric Arrangement: Triangular numbers can be visualized as dots arranged in equilateral triangles.

Relationship with Other Number Sets: 

Triangular numbers, while a unique sequence on their own, also exhibit interesting relationships with other number sets and mathematical concepts. Here are some of the notable relationships:

• Square Numbers:

The difference between any two consecutive square numbers is always a triangular number. For example, the difference between 4 (22) and 9 (32) is the triangular number 5. This relationship highlights the connections between the properties of square and triangular numbers.

• Polygonal Numbers:

Triangular numbers are a subset of polygonal numbers, which are figurate numbers representing patterns of dots that can be arranged to form regular polygons. The nth triangular number can be seen as a polygonal number with n sides (a triangle).

• Pascal's Triangle:

The triangular numbers are related to Pascal's Triangle. The nth row of Pascal's Triangle contains the coefficients of the binomial expansion of (a + b)n, and the sum of the coefficients in the nth row is the nth triangular number.

Examples of Triangular Numbers

Let’s solve some examples to gain more understanding of triangular numbers.

Example 1:

Find the 6th triangular number.

Solution:

The formula to calculate the nth triangular number is

 Tn = n × (n + 1) / 2.

For n = 6:

T₆ = 6 × (6 + 1) / 2

= 6 × 7 / 2

= 42 / 2

= 21

Therefore, the 6th triangular number is 21.

Example 2:

Compute the sum of the first 4 triangular numbers.

Solution:

The formula to calculate the sum of the first n triangular numbers is:

Sum = n × (n + 1) × (n + 2) / 6.

For n = 4:

Sum = 4 × (4 + 1) × (4 + 2) / 6

= 4 × 5 × 6 / 6

= 120 / 6

= 20

The sum of the first 4 triangular numbers is 20.

Example 3:

Let's consider the first two consecutive square numbers, 1 and 4, and demonstrate that the difference between these two square numbers is a triangular number.

Solution:

Square of 1 = 1² = 1

Square of 2 = 2² = 4

Difference = 4 - 1 = 3

Now, let's check if the difference, 3, is a triangular number using the formula

Tn = n × (n + 1) / 2.

For n = 2:

T2 = 2 × (2 + 1) / 2 = 3

Since 3 = 3.

We have successfully demonstrated that the difference between the first two consecutive square numbers (4 and 1) is indeed a triangular number (3).

These examples should provide a clearer understanding of how to calculate and work with triangular numbers.