Inflection Point Calculator

Inflection Point Calculator

Inflection point calculator is an easy-to-use tool to determine the inflection points of the given function with steps.

What is the Inflection point?

The inflection point is a point on the graph where the function changes its behavior. The slope of the curve change from decreasing to increasing or increasing to decreasing. An inflection point is also known as a stationary point.
Interpretation of inflection point:

Let's a function g(x), then the function is

• Concave down at a point ‘a’ if and only if f’’(x) <0;
• Concave up at a point ‘a’ if and only if f’’(x) > 0;

Where f’’ is the second derivative of the function.

Graphically representation:

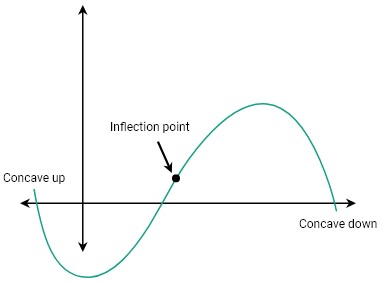
From the graph, we see that the graph shows two different trends before and after the inflection point.

 How to calculate the inflection point?

To find the inflection point we have to understand a numerical example given below

Example:

Find the inflection points of the function 2x^4-48x^2+22.

Solution:

Step 1: Take the first derivative of the function

f’(x) = 8x^3-96x

Step 2: Take the second derivative.

f’’(x) = 24x^2-96

Step 3: Now put the second derivative equal to zero.

24x^2-96=0

x^2=4

x=2,-2

Step 4: Check the function's behavior at x=2 put x=1 and 3.

f’’(1) = 24(1)^2-96= -72 (negative)

f’’(3) = 24(3)^2-96= 120 (positive)

Step 5: Check the behavior of the function at x=-2 put x=0 and -3.

f’’(0) = 24(0)^2-96= -96 (negative)

f’’(3) = 24(-3)^2-96= 120 (positive)

Step 6: Put 2,-2 in the second derivative.

f’’(x) = 24(2)^2-96 =0 

f’’(x) = 24(-2)^2-96 = 0

Hence the point of inflation is (2,0) and (-2,0).