To calculate result you have to disable your ad blocker first.
Jacobian Calculator
To find the Jacobian matrix, select variables, enter the functions in the required input boxes, and press the calculate button using Jacobian calculator
Table of Contents:
Jacobian Calculator
Jacobian calculator is used to find the Jacobian matrix & determinant after taking the derivative of the given function. This Jacobian matrix calculator finds the matrix for two and three variable functions.
What is the Jacobian matrix?
In vector calculus, the Jacobian matrix of multivariable-variable functions is the matrix of all its 1st-order partial derivatives.
The Jacobian matrix takes an equal number of rows and columns as an input i.e., 2x2, 3x3, and so on. In other words, the input values must be a square matrix. The determinant of the Jacobian matrix is referred to as the Jacobian determinant.
It is denoted by J and the entry (i, j) such as Ji,j = ∂fi/ ∂xj
Formula of the Jacobian matrix
Below is the general formula to find the Jacobian matrix.
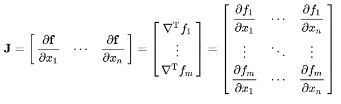
How to calculate the Jacobian matrix?
Below is a solved example of the Jacobian matrix.
Example
Find Jacobian matrix of x = x2 + 2y2 & y = 3x – 2y with respect to x&y.
Solution
Step 1: Write the given functions in a matrix.
x = x2 + 2y2
y = 3x – 2y
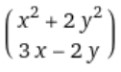
Step 2: Find the partial derivative of column 1 w.r.t “x” and column 2 w.r.t “y”.
∂/∂x (x2, 3x) = 2x, 3
∂/∂y (2y2, -2y) = 4y, -2
Step 3: Write the terms in the matrix form.
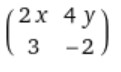
This is the required 2x2 Jacobian matrix of the given functions.
The determinant of this matrix is -4x -12y
Jacobian matrix = -4x – 12y
How to find the Jacobian of a 3x3 matrix?
Find Jacobian matrix of x = 3x3 + 4y2 – z2, y = 5x – 3y + 6z, and z = x + y + z with respect to x, y, & z.
Solution
To find the 3x3 Jacobian matrix, follow the below steps.
Step 1: Write the given functions in a matrix.
x = 3x3 + 4y2 – z2
y = 5x – 3y + 6z
z = x + y + z
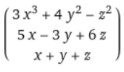
Step 2: Find the partial derivative of column 1 w.r.t “x”, column 2 w.r.t “y”, and column 3 w.r.t “z”.
∂/∂x (3x3, 5x, x) = 9x2, 5, 1
∂/∂y (4y2, -3y, y) = 8y, -3, 1
∂/∂z (z2, 6z, z) = 2z, 6, 1
Step 3: Write the terms in the matrix form.
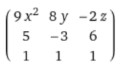
This is the required 3x3 Jacobian matrix of the given functions.
The determinant of this matrix is -81x2 + 8y – 16z
Jacobian matrix = -81x2 + 8y – 16z

