Lagrange Multiplier Calculator

Lagrange Calculator

Lagrange multiplier calculator is used to evaluate the maxima and minima of the function with steps. This Lagrange calculator finds the result in a couple of a second. 

What is the Lagrange multiplier?

The method of Lagrange multipliers, which is named after the mathematician Joseph-Louis Lagrange, is a technique for locating the local maxima and minima of a function that is subject to equality constraints.

(i.e., subject to the requirement that one or more equations have to be precisely satisfied by the chosen values of the variables).

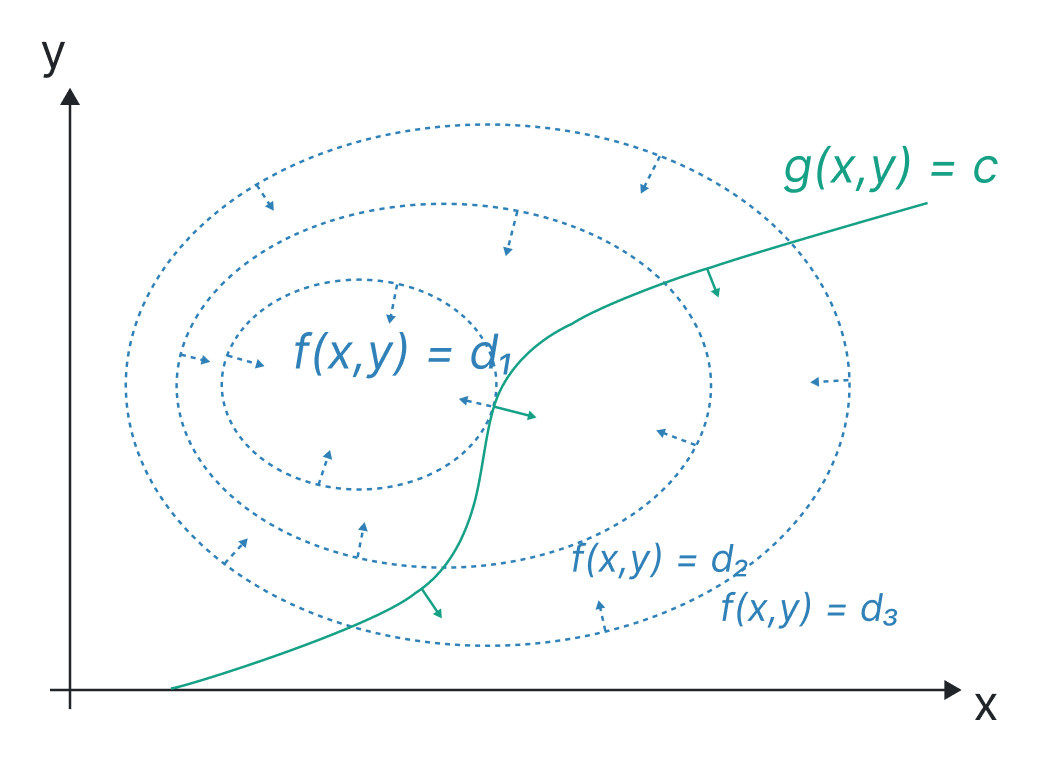
The fundamental concept is to transform a limited problem into a format that still allows the derivative test of an unconstrained problem to be used.

The Lagrangian function is a reformulation of the original issue that results from the relationship between the gradient of the function and the gradients of the constraints.

The formula for the Lagrange multiplier

The formula of the Lagrange multiplier is:

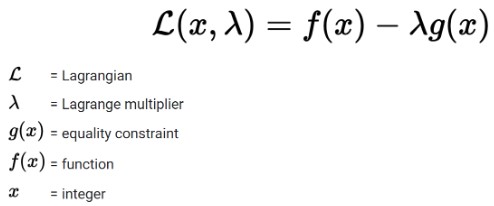
Example of Lagrange multiplier

Use the method of Lagrange multipliers to find the minimum value of g(y, t) = y² + 4t² – 2y + 8t subjected to constraint y + 2t = 7

Solution:

Step 1: Write the objective function and find the constraint function; we must first make the right-hand side equal to zero.

g(y, t) = y² + 4t² – 2y + 8t

The constraint function is y + 2t – 7 = 0

So h(y, t) = y + 2t – 7

To minimize the value of function g(y, t), under the given constraints.

g(y, t) = y2 + 4t2 – 2y + 8t corresponding to c = 10 and 26.

Step 2: Now find the gradients of both functions.

∇g(y, t) = (2y - 2)i + (8t + 8)j

∇h(y, t) = i + 2j

Now equation ∇g(y, t) = a∇h(y, t) becomes

(2y-2)i + (8t + 8)j = a(i + 2j)

Step 3: Compare the above equation.

2y - 2 = a

8t + 8 = 2a

Step 4: Now solve the system of the linear equation.

t= 1 and y= 5

Step 5: Evaluate the function

g(y, t) = 5²+ 4(1)² – 2(5) + 8(1) = 27

So h has a relative minimum value is 27 at the point (5,1).

Use our  Lagrangian calculator above to cross-check the above result.