System of Equations Calculator

System of Equations Calculator

System of Equations Calculator is a tool that is used to solve the system of linear equations simultaneously. To solve the system of linear equations, this calculator uses the substitution method and elimination method.

What is a system of equations?

A system of equations is a collection of linear equations that are to be solved simultaneously. The values of the variables that satisfy all of the equations in the system would be evaluated by solving a system of linear equations. 

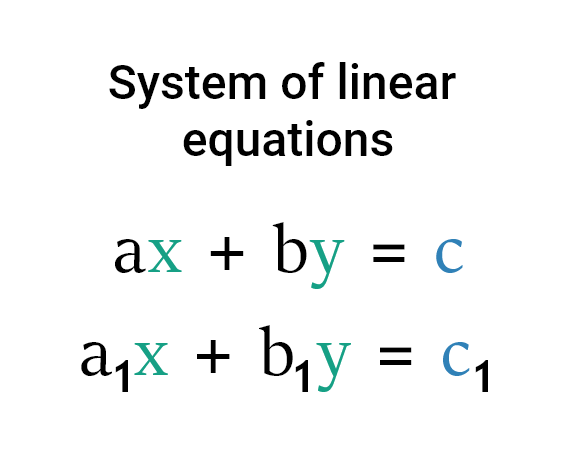
There are two well-known methods to solve the system of linear equations.

• Elimination Method
• Substitution Method

What is Substitution Method?

This method is used to solve a system of linear equations by substituting the value of one variable. Find the value of one variable (say “x”) which is dependent on another variable (say “y”) by one equation and substitute it into the other equation. To solve the system of linear equations by substitution follow the below steps.

• Take one equation from the linear system and solve it for one variable in terms of another.
• Substitute the above variable value in the other equations and eliminate the variable's value using some arithmetic operations.
• Solve the equation formed in the first step by using any of the variable values already found in the above steps.

Example of substitution method

Solve the following system of linear equations by substitution method.

x + 3y = -4

4x - y = 1

Solution:

Step 1: write the above equation and give the name eq (i) & eq (ii).

x + 3y = -4 ------> (i)

4x - y = 1--------> (ii)

Step 2: Solve the eq (i) for “x”.

x + 3y = -4

x = -4 -3y

Step 3: Substitute the above value in eq (ii) and Simplify for “y”.

Put x = -4 -3y in (4x - y = 1)

4(-4 -3y) – y = 1

-16 – 12y - y = 1

-16 – 13y = 1

– 13y = 1 + 16

– 13y = 17

  y = 17/(-13)

y = - 17/13

Step 4: Put the above value of “y” in step 2 and simplify.

y = - 17/13 in (x = -4 -3y)

x = - 4 – 3 (-17/13)

x = - 4 + (51/13)

Solve it by taking the LCM of the right side.

x = (-52 + 51)/13

x = -1 / 13

Hence

x = -1 / 13, y = - 17/13 is the solution of the given system of linear equations.

What is the elimination method?

In this method, we eliminate the variable making the same coefficient by some algebraic operation (multiply or divide). Some steps to eliminating the value of the variable are given below.

• Take the variables that you want to eliminate from the equation and make the coefficients of the variable same.
• Find the LCM of selecting a variable by choosing coefficients from all equations.
• Multiply both sides of all equations with the LCM to make the same coefficients.
• According to the situation add or subtract the equation to cancel the selected variable.
• By the above step, we get the value of one variable and use this value in any equation to find the value of the eliminated variable.

Example of elimination method

Solve the following system of linear equations by elimination method.

2x – y = 3, x + 2y = 2

Solution:

Step 1: Select the variable that wants to eliminate and write the above equation by assigning its name.

2x – y = 3------> (i)

x + 2y = 2------> (ii)

Eliminate the “y” to get the solution of the system in an easy way.

Step 2: Multiply by “2” with eq (i) on both sides and we get.

2(2x – y) = 2(3)

4x – 2y = 6

Step 3: Subtract the above equation with equation (ii) and simplify to eliminate the “y”.

 4x – 2y = 6

 x + 2y = 2

5x + 0y = 8

5x = 8

x = 8/5 = 1.6

Step 4: Put the above value of “x” in equation (ii) and simplify to find the value of “y”.

x = 8/5

x + 2y = 2

8/5 + 2y = 2

 2y = 2 – (8/5)

Take the LCM of the left side.

2y = 2 – (8/5)

2y = (10 – 8) / 5

2y = (2) / 5

y = (2) / (5)(2)

y = 2/10

y = 0.2

Hence,

x = 1.6, y = 0.2 is the solution of a given system of equations.