Binomial Theorem: Statement, Formula, Applications, and Examples

In the world of mathematics and algebra, the Binomial theorem is one concept that has proven to be an incredibly powerful and useful theorem.  This theorem gives us a systematic way to expand expressions involving binomials, which are algebraic expressions with two terms.

This theorem helps students and teachers to solve and simplify complex expressions, and equations, and explore the attractive world of algebraic operation. In this article, we’ll deep into the formula, expansion, and problems of the binomial theorem.

Statement of Binomial Theorem

The binomial theorem is a basic concept in algebra that provides a systematic way to expand expressions of the form (a + b)ⁿ, a, and b may be real numbers or variables and is a positive integer.

Binomial Theorem Formula

The binomial theorem formula is:

Binomial Coefficients

Binomial coefficients are crucial to the binomial theorem. They denote the number of ways to choose “r” items from a set of "n” to distinct items without considering their order. It can be calculated as:

Exponents in the Binomial Expression

The binomial expansion’s exponent follows a specific pattern. The exponent starts with n and decreases by tone with each subsequent term, while the exponent of b starts with 0 and increases by one. The result of the sum of exponents a and b in each term is always equal to n.

Pascal’s Triangle:

The triangular arrangement of numbers where each number is the sum of the two numbers directly above it is called Pascal’s triangle. Pascal’s triangle can be used to find the coefficients of the expanded form of binomial expressions.

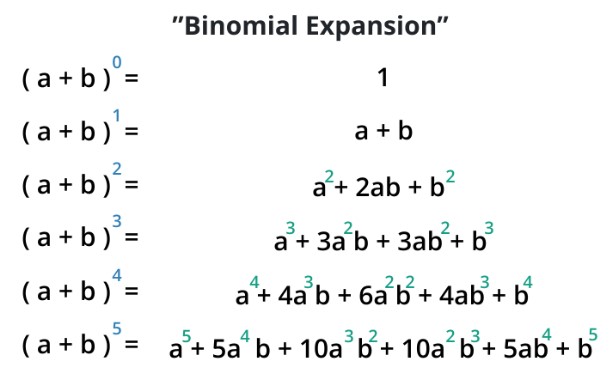
Steps to Expand Binomial Expressions Using the Binomial Theorem

To expand a binomial expression, follow the below steps.

1. Find the binomial coefficients.
2. Write out the terms of the expansion, one term at a time.
3. Multiply each term by the corresponding binomial coefficient.
4. Add up the terms to get the expanded expression.

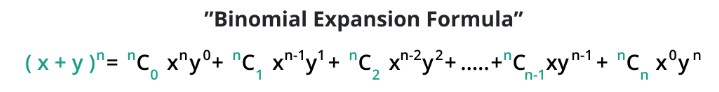
How to Expand Binomial Expressions?

Here are some examples of binomial expansion.

Example 1:

Expand the given binomial expression (x + 4)³.

Solution:

We use the following steps to expand the given binomial expression.

(x + 4)³ = x³ + (3x²) × (4) + (3x) × (4²) + 4³

= x3 + 12x2 + 48x + 64 (by binomial theorem) which is given above.

Step 1: Find the binomial coefficients.

Binomial coefficient for n = 4 

³C₀ = 1

 ³C₁ = 3

³C₂ = 3

³C₃ = 1

Step 2: Write out the terms of the expansion, one term at a time.

(x+ 4) ³ = x ³ + (3 x ²) × (4) + (3 x) × (4 ²) + 4³

Step 3: Multiply each term by the corresponding binomial coefficient

X³ + (3x²) × 4 + (3x) × 4² + 4³

Step 4: Add up the terms to get the expanded expression.

(x + 4)3 = x3 + 12x2 + 48x + 64

Example 2:

Expand the given term (2a - 3b)⁴

Solution:

Using the binomial theorem formula we have,

(2a - 3b) ⁴ = (⁴C₀) × (2 a) ⁴ × (-3 b) ⁰ + (⁴C₁) × (2 a) ^4-1 × (-3 b) ¹ + (⁴C₂) × (2 a) ^(4-2) × (-3 b) ² + (⁴C₃) × (2 a) ^4-3) × (-3 b) ³ + ⁴C₄ × (2 a) ⁰ × (-3 b) ⁴

Simplifying further:

(2a - 3b)4 = 16 a4 – 96 a3b + 216 a2 b2 – 216 ab3 + 81 b4

Applications of Binomial Theorem:

The binomial theorem has a wide range of applications such as science, and engineering some of them are as follows.

Solving Equations

We used the binomial theorem to solve equations that involve the powers of binomial expressions. For example, the equation (a + b)2 = 9 can be solved using the binomial theorem to get a2 + 2ab+ b2 = 9.

Finding probabilities

We can use the binomial theorem to find probabilities of events that involve multiple trials. For example, the probability of tossing a coin 5 times and getting heads 3 times can be found using the binomial theorem.

Calculating areas and volumes

The binomial theorem can be used to calculate areas and volumes of shapes that are made up of multiple smaller shapes. For example, the area of a triangle can be found using the binomial theorem