Derivatives – What are they and how to solve them?

Before learning about derivatives, you need to have a clear concept of limits, Slope, and how to find them.

Why do we need derivatives?

The slope represents a change of y with regards to x on a straight line. It is the same at every point of a line. But, certainly, this is not the case with a curve line.

So, how do you find the slope of a curve line? It is found by calculating the slope of the secant line passing through two points of the curve.

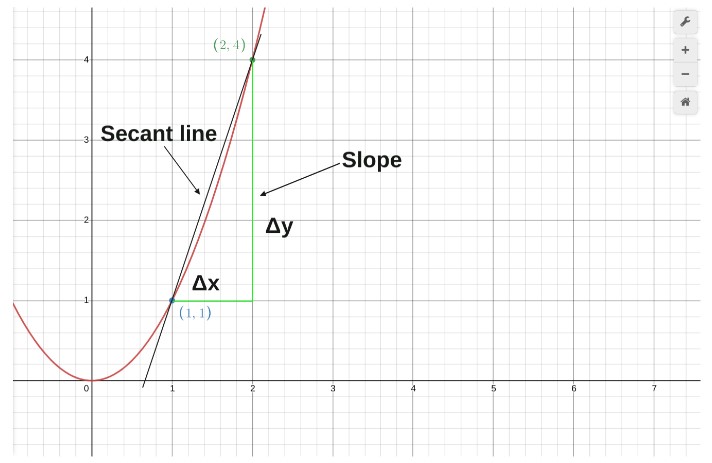
Above is a graph of the function of x². We drew a secant line to find the slope between point (1,1) and point (2,4),

The slope is 3. We found it using the slope formula calculator. This slope is the average slope between these points.

But what if we wanted to find the slope of a point at the exact point (1,1), the instantaneous rate of change? How can we do this?

This is where we use derivatives!! Let’s learn more about derivatives and how to solve them.

What are Derivatives?

Derivatives are used to find the slope of a curve line at an exact point. Definition of derivatives would be:

“The derivative of a function can be interpreted as the slope of the graph of the function or, more precisely, as the slope of the tangent line at a point.”

In calculating derivatives, we find the differential of a function. Meaning here that, we find the difference between the two points.

These points are placed so closely together that the difference between them is almost zero and the secant line between them becomes the tangent line.

Notations

Derivatives are notated in three different ways. The most common way is Labinez’s notation.

How to find Derivatives?

Hopefully, now your confusion about derivatives and why we use them is clear. Let’s move on to the calculation of derivatives.

There are two main ways by which derivatives are solved. One is formal and the other is an alternate form. We will learn both with general examples.

The Formal Differentiation

It will be easy to derive a formula for derivatives while looking at a graph.

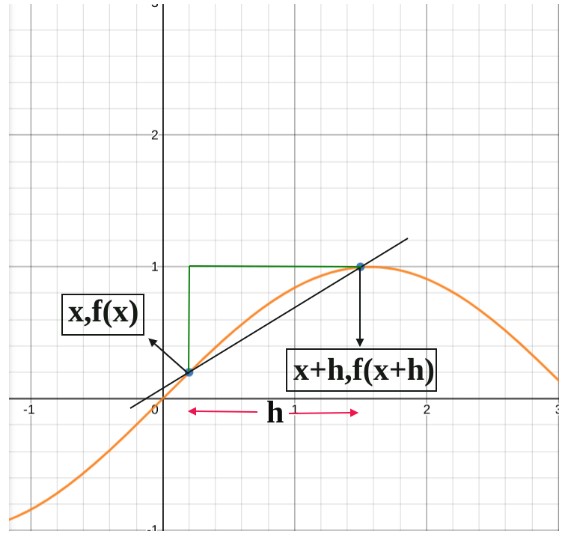
Consider a sinusoidal function. We want to calculate the slope between two points on this curve. The first point is at x. As we know y=f(x), we can write the point as (x,f(x)).

We will take the second point at a distance of h from x. The point here will be (x+h,f(x+h)), where h is an arbitrary value. It could be any number.

Slope at this point is:

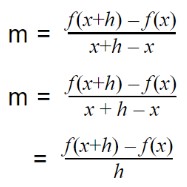
 As we want to calculate the slope of the exact point, we will bring the two points so close together that they almost become one point and the difference between them approaches zero.

For this purpose, we will apply a limit on this function. The equation becomes like this:

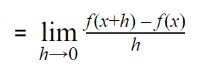
This is what we will call derivative or d over dx (d/dx). Now, we can substitute any value at the place of x.

So this was one way to calculate the derivative or find the slope at a pinpoint. Let’s move on to the second and alternative formula of differentiation.

Note: Usually in calculus,  replaces h. Delta means a very small change. The slope formula with  is:

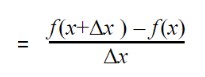
Alternate Form

This is quite similar to the first formula. But here instead of adding a distance to x, we will take a whole different point (a,f(a)). Let’s see its graph:

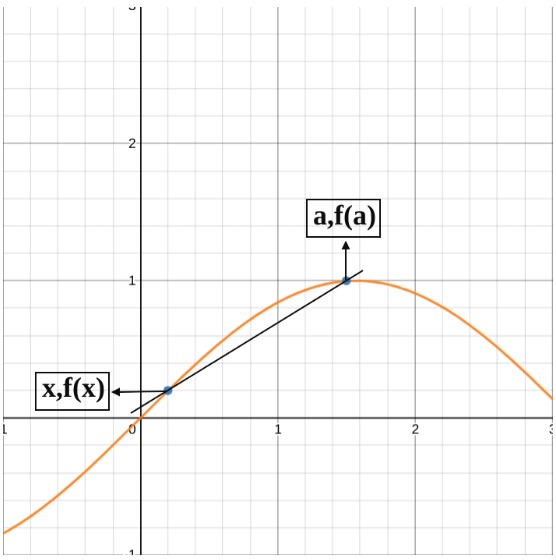
By applying the slope formula, the equation will be:

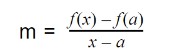
By applying limit:

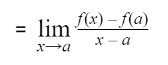
This is the same thing as the formal way. Here, instead of taking a distance h, we took a direct point a. So when x approaches a the distance will be almost zero. And this is exactly what we want to calculate.

Example

Find the derivative of f(x) = x².

Solution:

Step 1: Add the distance of in the x². This distance of delta x is approximately zero. We will now find the function for (x + )².

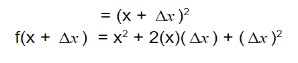
Step 2: Applying slope formula is:

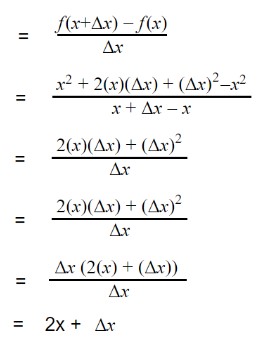
Step 3: Apply limit  approaches to zero.

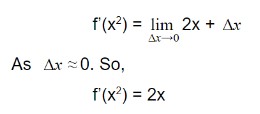
Hence, the slope at x² = 2x.

What is the derivative of x⁴? Find it yourself and verify using the derivative calculator.

Rules of Differentiation

Differentiation is made easy with some rules. These rules are applied in certain situations to dodge complex and lengthy calculations. The main and basic rules are explained below.

Constant Rule

It is probably the simplest derivative rule. When we don’t have a variable in a function e.g y=4, then the derivative is 0.

                                                f’(c) = 0            

Where c is a constant number. This rule makes sense if you try to visualize it.

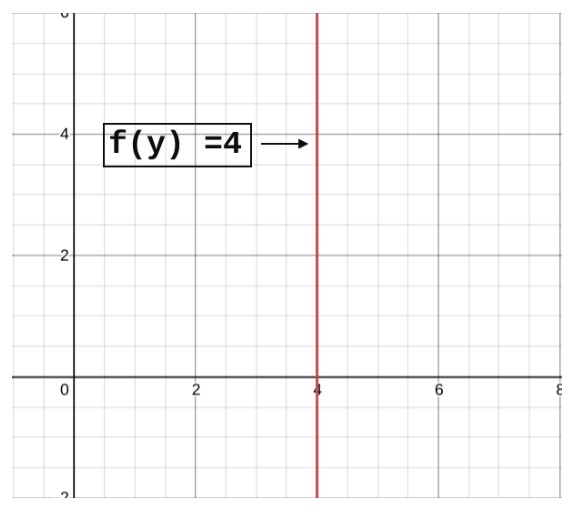
Since x = 0, hence there is no slope. And the graph is a straight vertical line. But let’s see this with the help of differentiation.
Example

What is the derivative of f(x) = 5.

Solution:

Step 1: Add delta x.

    f(x + Δx)  = 3 + Δx = 3                             Δx = 0

Step 2: Apply formula.

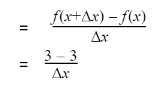
= 0/Δx

= 0

Power Rule

The power rule is applied to polynomial functions. The formula is:

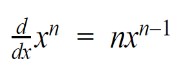
The example of f(x²) we solved to learn derivatives is a perfect representation of the power rule. But for more understanding, see another example:

Example:

Derivative of x⁶. Solve this using limits as well as power rules.

Solution:

Solving using limits.

Step 1: Add delta x i.e and expand the equation.

                       = (x + Δx)⁶

      f(x + Δx)⁶ = (x⁶ + 6x⁵ Δx + … + Δx⁶)

Step 2: Apply the formula of the slope.   

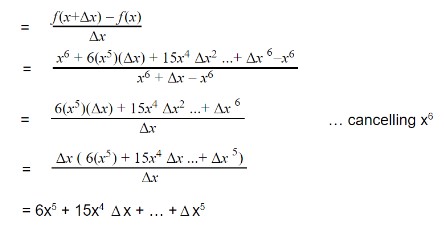
Step 3: Apply limit.

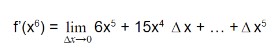
Solving using power rule.

Step 1: Write the function.

f(x) = x⁶

Step 2: Identify the components and apply the power rule.

As yⁿ = ny^n-1,     (we formed the formula with y to remove any confusion.)

Here,     y = x

n = 6

Applying the rule;

 f’(x⁶) = (6)x^6-1 = 6x⁵

The results of both methods are the same. This proves that the power rule is true for any n.

Sum and Difference Rule

Two functions in addition or difference are also eligible for a differentiation rule. The rules applied in such situations are;

For sum:

f + g = d/dx (f) + d/dx (g)

For difference.

f - g =  d/dx (f) - d/dx (g)

Example:

Find f’(x) for 2x + 3x².

Solution:

Step 1: Apply derivative.

= d/dx ( 2x + 3x²)

Step 2: Apply the rule.

=  d/dx 2x + d/dx 3x²

=   2.1x^1-1 + 3.2x^2-1                      Applying the power rule.

=   2 + 6x   

Product Rule

When the derivative of two functions in multiplications is computed, we then use the product rule. An example of such a function will be  4x⁴(3x + 9).

The formula of product rule is:

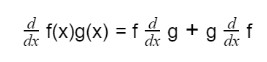
Example:

What is the derivative of 4x⁴(3x + 9)?

Solution:

Step 1: Apply derivative. 

= d/dx 4x⁴(3x + 9)

According to the product rule.

=  4x⁴ d/dx (3x + 9) + (3x + 9) d/dx 4x⁴

Step 2: Solve for d/dx (3x + 9).

d/dx = (3x + 9)

Apply sum rule.

= d/dx 3x + d/dx 9

= 3 + 0        … (power rule for 3x and constant rule for 9)

= 3

Step 3: Solve for d/dx 4x⁴.

Using power rule;

= 4.{(4)x^4-1}

= 4.4x³

= 16x³

Step 4: Put the values and simplify.

= 4x⁴.3 + (3x +9)16x³

= 12x⁴ + 48x⁴ + 144x³

= 60x⁴ + 144x³

= x³(60x + 144)

Quotient Rule

We have a formula for product but do we have a formula for division? Yes! And It is called the quotient rule. It is mainly derived from product rule for differentiation.

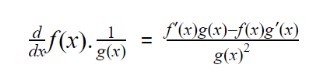
A quotient equation looks something like this: f(x)/g(x). To find its derivative, it is divided into two parts: f(x) * 1/g(x). You can see that actually, we have to perform the product rule.       

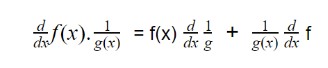
All we need to do is to find the derivative of 1/g(x). Following all the familiar process of applying formula and limit, we will get:

Note that,

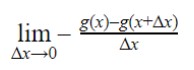
is the dg/dx with a negative sign.           

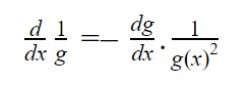
Or it can be written as: 

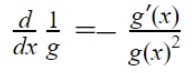
Now on putting this value in the product formula we discussed above:

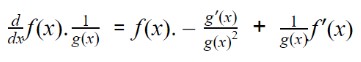
Taking LCM.

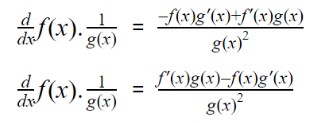
This is the quotient rule.

Example:

Find the derivative of (x - 3)/(x³ + x).

Solution:

Directly apply the quotient rule.

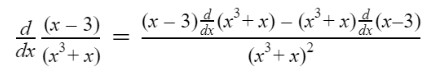
Step 1: Find the derivative of (x-3).

= d/dx (x-3)

= 1 

Step 2: Find derivative of (x³-x)

= d/dx (x³-x)

Using the rules discussed above;

= 3x² - 1

Step 3: Use these in the main equation.

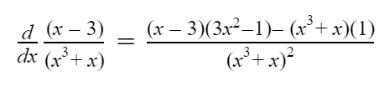
After simplifying;

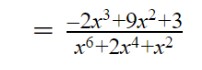
Chain Rule

Last but not the least, we have the chain rule. It states that:

This is for simplicity's sake. When a function has many mathematical operations, it is better to convert it in terms of two functions e.g, we have a function:

f(x)= (X² + 6)⁴

Let g =X² + 6, then

f(g) = (g)⁴  where g =X² + 6  

OR

f(g(x)) = (X² + 6)⁴

To find its derivative, you first find the difference of f with respect to g and then g’(x). After that, multiply.

Example:      

Solve d/dx (X² + 6)⁴

Solution:

Let g(x) = x² + 6

And f(g) = g⁴

So the derivative of f(g(x)) = d/dx f(g(x)) =f’(g(x)).g’(x).

Applying the chain rule.

Step 1: Find the derivative of g(x).

d/dx = x² + 6            … using power rule for x² and constant rule for 6

 = 2x

Step 2: Find the derivative of f(g).

= d/dx g⁴

= 4g³

Step 3: Putting in the formula and multiplying.

= 4(x²+6)³. 2x

= 8x.(x²+6)³           

Implicit Differentiation

Since you now have an idea about solving derivatives. It is about the right time we see how to perform implicit differentiation.

Implicit differentiation is simple differentiation except that it is performed on both sides of the equation.

Example:

Differentiate this implicit equation:

    x² + y² = z²

Where z is constant.

Solution:

Step 1: Apply derivative.

d/dx (x²) + d/dx(y²) = d/dx(z²)

Step 2:  Solve L.H.S.

= d/dx (x²) + d/dx(y²)

= 2x + 2y(d/dx)                  … applying chain rule.

Step 3: Solve R.H.S.

The derivative of constant numbers is 0.

= d/dx (z²)

= 0

Step 4: put the values in the equation.

2x + 2y(d/dx) = 0

2y(d/dx) = -2x

y(d/dx) = -x

d/dx = -x/y

So, on performing differentiation on equation  x² + y² = z², we got -x/y as derivative.

Summary

We use derivatives to find the slope of a curve line. It is the process of differentiation. It is a complex process so we make use of rules of differentiation.