To calculate result you have to disable your ad blocker first.
Combination Calculator
Plugin the values of n(total elements) and r(selected elements) in the combinations calculator.
Combination Calculator
Combination calculator is used in different fields like physics, statistics, and math. The function of the combination calculator is to find the total number of possible subsets you can have from a superset.
These sets will have combinations without repetition. The ncr calculator uses the established combination formula.
What is a combination?
The definition of combinations in mathematics states:
“The total number of possible outcomes you can have using r number of elements that are a part of a set containing n elements.”
A lot to take in, huh? Worry not because it will be discussed in detail through an example.
Suppose you want to buy three pieces of furniture: bed, desk, and wardrobe. But you can afford only two. This gives you a choice of three sets: (bed, desk), (desk, wardrobe), (wardrobe, bed). So you see what set suits you the most.
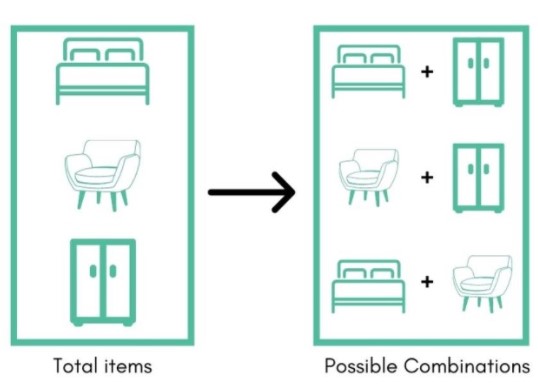
Now it does not matter if you place the bed first and the wardrobe later because, in the end, you will have both pieces. This is a perfect example of a combination.
Combination Formula
The formula used for combinations is:
= n!/r!(n-r)!
In this formula, n stands for the total elements and r stands for the selected elements. The operator used (i.e !)is called factorial.
Combinations are denoted by nCr which is read as “n choose r”.
Fact time: Analyzing for some time on the combination formula reveals that “n choose 1” is equal to n combinations and “n choose n” is equal to 1 combination.
Combination and permutation
The main difference between these two terms is the order of the elements. In combination, it does not matter which value you place first in the set. But in permutation, it is essential to keep the order of things in view.
An example can help a lot to understand. Assume you have digits 3, 4, and 5. The possible 6 sets can be (3,4,5), (3,5,4), (4,3,5), (4,5,3), (5,3,4), (5,4,3).
Now the arrangement of these digits is important if you use them as a password for your briefcase or device. In that case, all of these sets are different. This is a permutation example.
But if these digits are numbers of players’ shirts and you are forming a group of three, then it does not matter. Because eventually all three of them will be in the group. This is a combination example.
This also explains the difference between combination and permutation formulas.
Did you know? A combination lock is actually a permutation lock because the order of the digits matters in it.
Take a minute to check our arithmetic sequence calculator.
How to find combinations?
You can try our ncr formula calculator for this purpose. Other than that, combinations can be found manually as well. But it gets tougher for larger values.
Example:
Alex has 6 colorful balls in a bag. If he draws three balls out what could be the possible number of combinations of colors he draws. Also, write the combinations.
Solution:
Suppose that the colors are A, B, C, D, E, and F.
Step 1: Identify the values.
n = 6
r = 3
Step 2: Use the formula.
= n!/r!(n-r)!
= 6!/3!(6-3)!
= 6!/3!(3)!
= 720/(6 * 6)
= 720/36
= 20
Hence, there are 20 possible combinations. Those combinations are:
ABC, ABD, ABE, ABF, ACD, ACE, ACF, ADE, ADF, AEF, BCD, BCE, BCF, BDE, BDF, BEF, CDE, CDF, CEF, DEF.

