To calculate result you have to disable your ad blocker first.
Partial Fraction Calculator
To find rational fraction, enter function and click calculate button using partial fraction calculator
Partial Fraction Calculator
Partial fraction calculator is used to expand the polynomial rational functions with steps. This partial fraction decomposition calculator takes the numerator and denominator of a function to decompose that function.
What is the partial fraction?
In mathematics, a partial fraction is a method to write a rational function (quotient of two polynomials) as the sum of simpler rational expressions. It is also written as the sum of the fractions whose denominators are the linear binomials.
Formulas of partial fraction
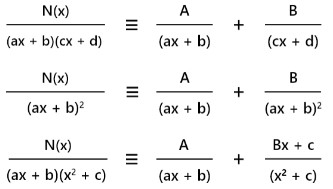
How to calculate the partial fraction?
Here is a solved example of the partial fraction.
Example
Find the partial fraction of (2x2 + 1)/(x+1)(x+5)
Solution
Step 1: Write the formula of the partial fraction.
F(x)/(ax+b)(cx+d) = A/(ax+b) + B/(cx+d)
Step 2: Substitute the given rational function.
(2x2 + 1)/(x+1)(x+5) = A/(x+1) + B/(x+5) … equation (1)
Step 3: Multiply by (x+1)(x+5) on both sides of the above expression.
(x+1)(x+5) * (2x2 + 1)/(x+1)(x+5) = (x+1)(x+5) * A/(x+1) + (x+1)(x+5) * B/(x+5)
(2x2 + 1) = A(x+5) + B(x+1)
Step 4: Put x = -1 in the above expression.
(2(-1)2 + 1) = A(-1+5) + B(-1+1)
(2(1) + 1) = A(4) + B(0)
(2 + 1) = 4A + 0
3 = 4A
A = 3/4
Step 5: Now Put x = -5.
(2(-5)2 + 1) = A(-5+5) + B(-5+1)
(2(25) + 1) = A(0) + B(-4)
(50 + 1) = 0 - 4B
51 = - 4B
B = -51/4
Step 6: Put the values of A & B in equation (1)
(2x2 + 1)/(x+1)(x+5) = 3(x+1)/4 - 51(x+5)/4

