Linear Regression Calculator

Linear Regression Calculator

Use the line regression calculator to find the regression equation. This linear regression calculator uses X and Y values to determine the regression equation. This tool also computes the following components required in the regression equation:

• Y-intercept 
• Mean of the dependent variables (y)
• Mean of the independent variables (x)
• Slope

Users can add more readings of x and y by clicking on “Add more” and on the way, these rows can be deleted as well.

What is linear regression?

Regression is a technique or ability to establish a mathematical relationship between two variables. One of these is dependent and the other is independent.

For example, the estimation of the dependence of food consumption on the monthly income of families. 
Linear regression involves only two variables. There is another type of regression, known as multiple regression. It includes more than two variables.

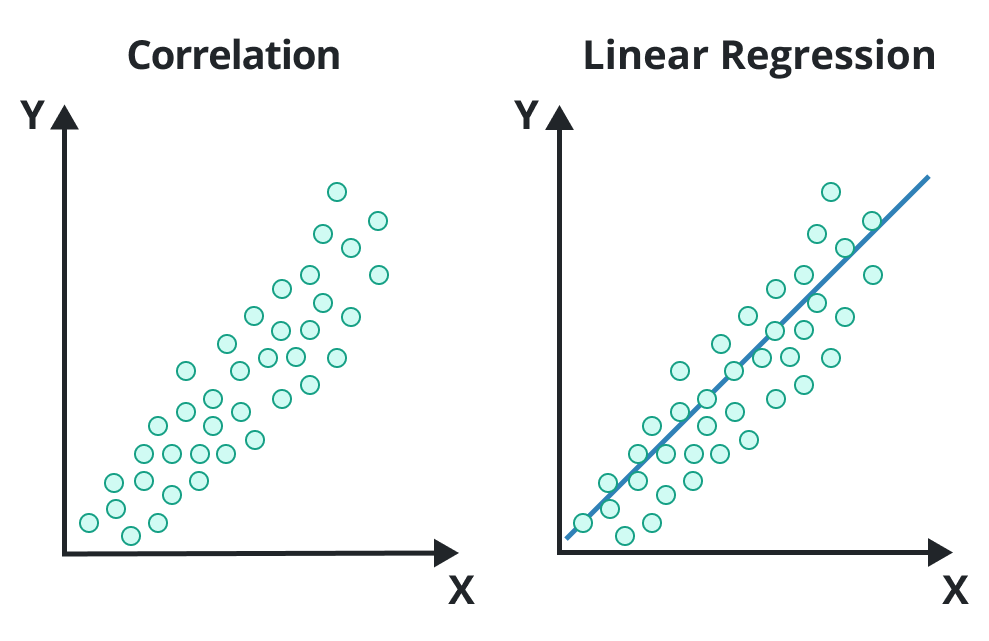
There is another objective of linear regression in statistics and that is the forecasting of the new observation. 

For example, from the previous data of a family’s increase in consumption with the increase in income, the prediction of the consumption increase if the income rises more this year.

Regression equation:

Before looking at the regression equation, it is important to know about the variables that lay down the foundation of it.

Variable X is usually taken as an independent variable and this is the one that explains the dependent variable. The dependent variable is Y in a bi-dimensional plane. It is one that we forecast. 

The general equation is:

• Yi = Dependent variable
• ꞵ0 = Population y-intercept
• ꞵ1 = Population Slope
• Xi = Independent variable
• Ɛi = Error term

In statistics, most of the techniques are designed to apply to the sample data. So the fitted equation will be;

ŷ = a + bx

Here:

• ŷ is the estimated value of y
• a is the sample y-intercept 
• b is the sample slope/regression coefficient 
• x is the independent variable

Now let’s move on to the computation of this equation.

How to calculate the regression equation?

There are two main values that you have to calculate to make the regression equation; y-intercept(a) and slope(b).

The slope has three formulas. The basic and easiest one is the one written below.

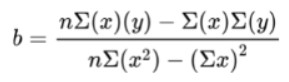
In this formula, the numerator is the covariance of x and y and the denominator is the variance of x.

To find the y-intercept, use the given formula.

a = ͞y - b ͞x

The ͞y and ͞x represent the mean of y and x respectively.

After finding both values, all you have to do is put them in the sample equation. To clear your concept, read the solved example below. 

Example:

Given these then pairs of (X, Y) values

X

1

1

2

3

4

4

5

6

6

7

 

Y

2.1

2.5

3.1

3.0

3.8

3.2

4.3

3.9

4.4

4.8

1. Find the regression equation.
2. Predict the value of Y when X=10.

Solution:

(a) Regression equation

Step 1: Find the slope.

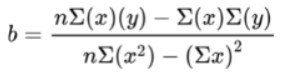
It will be easy to make a table and find the necessary values through it.

n= ?
Summation X = ?
Summation Y = ?
XY = ?
Summation XY = ?
X2 = ?
Summation X2 = ?

n	X	Y	(X)(Y)	X2
1	1	2.1	2.1	1
2	1	2.5	2.5	1
3	2	3.1	6.2	4
4	3	3.0	9	9
5	4	3.8	15.2	16
6	4	3.2	12.8	16
7	5	4.3	21.5	25
8	6	3.9	23.4	36
9	6	4.4	26.4	36
10	7	4.8	33.6	49

n   = 10

∑x = 1 + 1 + 2 + 3 + 4 + 4 + 5 + 6 + 6 + 7
     = 39

∑y = 2.1 + 2.5 + 3.1 + 3.0 + 3.8 + 3.2 + 4.3 + 3.9 + 4.4 + 4.8 
     = 35.1

∑xy = 2.1 + 2.5 + 6.2 + 9 + 15.2 + 12.8 + 21.5 + 23.4 + 26.4 + 33.6
       = 152.7

∑x2 = 1 + 1 + 4 + 9 + 16 + 16 + 25 + 36 + 36 + 49 
      = 193

Putting these values in the equation, we have;

b = [(10)(152.7) - (39)(35.1)] / [10 (193) - (39)2]
   = 158.1 / 409
   = 0.387

Step 2: Calculate the y-intercept. 

a = ͞y - b ͞x

Mean of Y = 35.1 / 10
                 = 3.51

Mean of X = 39 / 10
                 = 3.9

Now, use this data in the intercept equation.
a = 3.51 - (0.387)(3.9)
    = 2.00

Step 3: Put both values in the regression equation.

ŷ = a + bx
ŷ = 2.001 + 0.387x

(b) Predict Y 

Step 1: Put the value of X in the computed regression equation.

ŷ = 2.001 + 0.387x
ŷ = 2.001 + 0.387 (10)
ŷ = 2.001 + 3.87
ŷ = 5.871