Chat with us
To calculate result you have to disable your ad blocker first.
Summation Calculator
Enter starting value, ending value, equation, and variable to find the sum of a function using sigma notation calculator.
ADVERTISEMENT
ADVERTISEMENT
Examples:
Click to calculate sigma notation
$${\large \sum_{ \small x=1}^{\small n=10} x^{(-1/3)}}$$
$${\large \sum_{ \small x=1}^{\small n=10} x^2+2*(cos(x)+\sqrt{x})}$$
$${\large \sum_{ \small x=1}^{\small n=10} 2x*(x-1)!}$$
$${\large \sum_{ \small x=1}^{\small n=10} cos(pi*x/10)}$$
Summation calculator with Sigma Notation (Σ)
Summation calculator is an online tool that calculates the sum of a given series. It can find the Sigma notation sum of any function. This summation notation calculator also shows the calculation with steps.
What is summation?
Summation is the process of the addition of a sequence of any type of number. Besides numbers, other types of values such as functions, matrices, and vectors can be summed as well.
Summation is denoted by the Greek letter Sigma notation Σ.
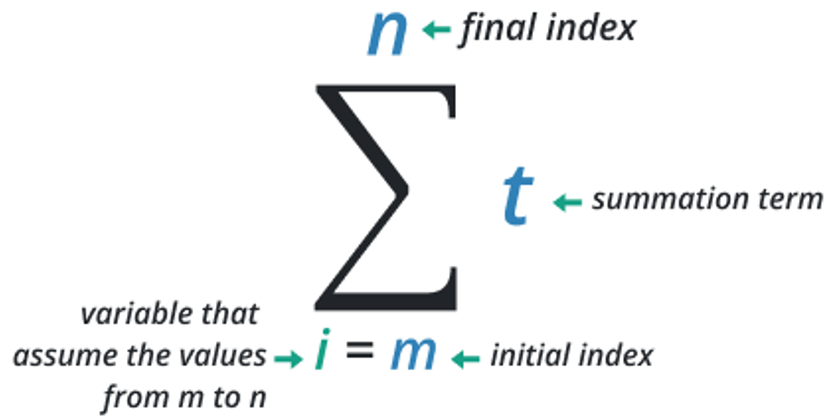
Summation notation formula
The equation to find the sum of the series is given below.
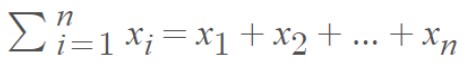
Where,
iis the starting value, andnis the upper limit.
Types of summation
There are two types of summation.
- Simple summation
- Sigma Notation
| Type Name | Statement | Expression |
| Simple Summation | It is used to add numbers or quantities arithmetically. It can also be referred to as the algebraic sum of numbers or quantities. | 1+2+3+4=10 |
| Sigma Notation | The sigma notation is used to evaluate the sum of the function by placing the lower and upper limit values. The lower limit of the summation is said to be the index of the given expression. While the upper limit is said to be the endpoint of the given expression. The problems of the sigma notation can also be solved with the help of our sum of series calculator for well-known functions such as | $${\sum _{i=0}^n\left[f\left(x\right)\right]}$$ |
How to evaluate summation?
To calculate summation notation, follow the example given below.
Example 1:
Find the sum of the first 10 prime numbers
Solution
Step 1: Write the first 10 prime numbers along with the addition sign between them.
2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29
Step 2: Now evaluate the sum of the series of prime numbers.
2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29 = 129
Hence the sum of the first 10 prime numbers is 129.
Example 2:
Evaluate summation for the function (x + 2)2 with an upper limit of 10 and a starting value of 4.
Solution:
Step 1: First of all, let’s identify the values.
x = 4, n = 10
Step 2: Place the given function in the summation equation.
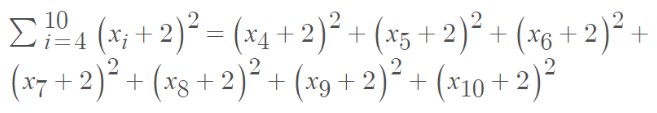
Step 3: Substitute the series values in the above equation.
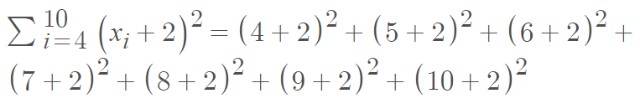
Step 4: Simplify the equation.
Different formulas for calculating summations
Summation for | Formula |
Sum of natural numbers | mΣx=1 x = [m(m + 1)]/2 |
Sum of squares of natural numbers | mΣx=1 x2 = [m(m + 1)(2m + 1)]/6 |
Sum of cubes of natural numbers | mΣx=1 x3 = [m2(m + 1)2]/4 |
Sum of 4th power of natural numbers | mΣx=1 x4 = [m(m + 1)(2m + 1)(3m2 + 3m – 1)]/30 |
Sum of 1st m even numbers | mΣx=1 2x = m(m + 1) |
Sum of 1st m odd numbers | mΣx=1 (2x + 1) = m2 |
Sum of an arithmetic sequence | mΣx=1 a + (x – 1)d = m[2a + (m – 1)d]/2 |
ADVERTISEMENT