To calculate result you have to disable your ad blocker first.
Asymptote Calculator
Enter the function f(x) in asymptote calculator and hit the Calculate button.
Table of Contents:
Asymptote Calculator
The asymptote finder is the online tool for the calculation of asymptotes of rational expressions. Find all three i.e horizontal, vertical, and slant asymptotes using this calculator.
The user gets all of the possible asymptotes and a plotted graph for a particular expression.
What are Asymptotes?
Asymptotes are approaching lines on a cartesian plane that do not meet the rational expression understudy.
By looking at their graph, one can make the assumption that they will eventually meet, but that’s not true (except horizontally). Asymptotes converge toward rational expression till infinity.
See another similar tool, the limit calculator.
Types of Asymptotes
Asymptotes are further classified into three types depending on their inclination or approach.
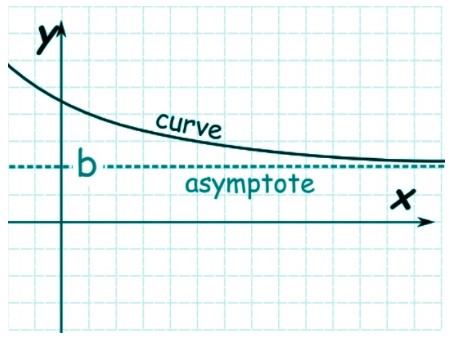
1. Horizontal asymptotes move along the horizontal or x-axis. The line can exist on top or bottom of the asymptote.
Horizontal asymptotes are a special case of oblique asymptotes and tell how the line behaves as it nears infinity. They can cross the rational expression line.
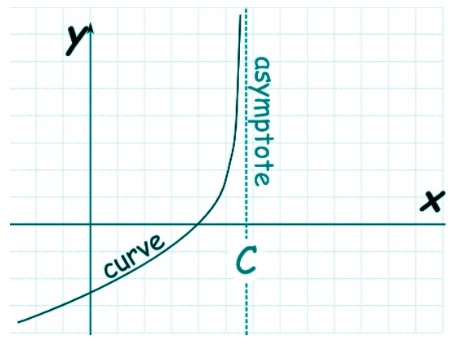
2. Vertical asymptotes, as you can tell, move along the y-axis. Unlike horizontal asymptotes, these do never cross the line. But they also occur in both left and right directions.
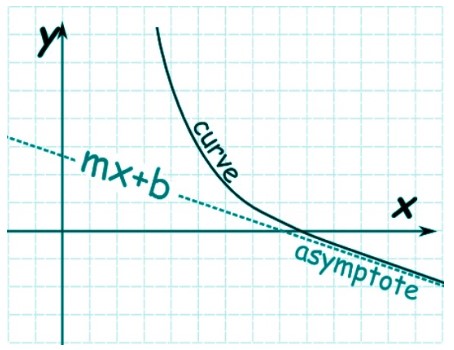
3. The last type is slant or oblique asymptotes. It has some slope, hence the name. This asymptote is a linear equation with a value equal to y=mx+b.
That accounts for the basic definitions of the types of the asymptote. Now, let’s learn how to identify all of these types.
Note that it is possible for a rational expression to have no asymptote converging towards it.
How to find asymptotes?
Try using the tool above as the horizontal, vertical, and oblique asymptotes calculator. But there are some techniques and tips for manual identification as well.
We will learn their process one by one.
Horizontal asymptotes:
A rational expression can have one, at zero, or none horizontal asymptotes. To know which of the mentioned situations exist, the numerator and denominator are compared.
The two cases in which an asymptote exists horizontally are;
Case 1 (Higher denominator):
When the denominator of a rational expression is greater, in terms of degrees than the numerator. In other words when the fraction is proper then the asymptote occurs at y=0. That is along the x-axis.
Consider that you have the expression x+5 / x2 + 2. On comparing the numerator and denominator, the denominator appears to be the bigger expression.
This means the asymptote of this expression occurs at y=0.
Case 2 (equal degree):
A rational expression with an equal degree of numerator and denominator has one horizontal asymptote.
To know where this asymptote is drawn, the leading coefficients of upper and lower expressions are solved.
An example of this case is (9x3 + 2x - 1) / 4x3. As you can see the highest degree of both expressions is 3. Separate out the coefficient of this degree and simplify.
The horizontal asymptote occurs at 9/4.
If none of these conditions meet, there is no horizontal asymptote.
Slant/oblique asymptote:
Slant asymptotes are easy to identify but rather difficult to calculate. The only case left of a rational expression is when the degree of the numerator is higher than the denominator.
Again there are two possibilities.
Case 1 (one degree higher):
If the numerator surpasses the denominator by one degree then the slant asymptote exists. For example, if the degree of the numerator is 6 and the denominator has a degree of 5, then the asymptote will occur.
Since oblique asymptotes have a linear equation, the process is a little different than the horizontal asymptote. Perform the polynomial long division on the expression.
During this calculation, ignore the remainder and keep the quotient. See the example below.
Example:
Solve (2x2 + 7x + 4) / x - 3 to find the slant asymptote.
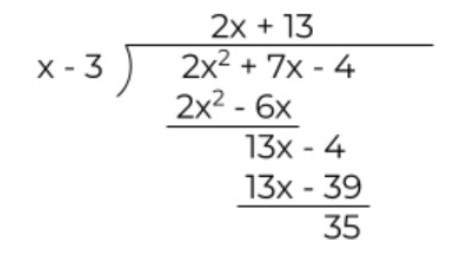
The quotient expression 2x + 13 is the value of y i.e. y = 2x + 13.
Case 2 (more than one degree higher):
When the numerator exceeds the denominator with more than one power e.g. 7x6 / 2x, in such a scenario, slant asymptote does not occur.
Vertical asymptote:
It is equally difficult to identify and calculate the value of vertical asymptote. Vertical asymptotes can be located by looking for the roots of the denominator value of a rational expression.
The value of roots is where the vertical asymptote will be drawn. You can find one, two, five, or even infinite vertical asymptotes (like in tan(x)) for an expression.
Basically, you have to simplify a polynomial expression to find its factors. For clarification, see the example.
Example:
Find the vertical asymptotes for (6x2 - 19x + 3) / (x2 - 36).
Take the denominator and factorize.
= (x2 - 36)
= x2 - 6x + 6x - 36
= x(x - 6) + 6(x - 6)
= (x - 6)(x + 6)
It is suggested to solve the numerator as well, in case any factors cancel out. Skipping to the final factors, we have 6x2 - 19x + 3 = (6x - 1) (x - 3). Since nothing is canceled, the asymptotes exist at x = 6 and x = -6.

