To calculate result you have to disable your ad blocker first.
Calculadora De Desvio Padrão
Insira dados de amostra ou população na caixa de entrada fornecida para encontrar o desvio padrão usando a calculadora de desvio padrão.
Calculadora de desvio padrão
A calculadora de desvio padrão é usada para encontrar o desvio padrão, variação , média e a soma estatística dos quadrados. Esta calculadora de desvio obtém uma amostra e um conjunto populacional de valores de dados.
Qual é o desvio padrão?
A medida da propagação da distribuição de dados é conhecida como desvio padrão . Ele mede a distância entre cada observação de dados e a média. O desvio padrão é de dois tipos:
- Desvio padrão da amostra
- Desvio padrão populacional
Se os dados fornecidos forem a própria população, divida a soma dos quadrados por N .
Se os dados fornecidos forem uma amostra de uma população maior, então a soma dos quadrados deve ser dividida por n – 1 .
Fórmula de desvio padrão
A fórmula para o desvio padrão da população é:
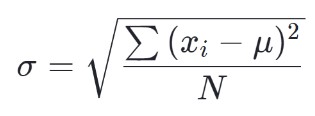
A fórmula para o desvio padrão da amostra é:
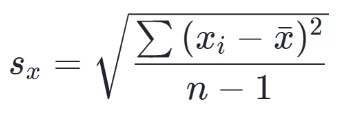
Como calcular o desvio padrão?
Abaixo estão alguns exemplos resolvidos para entender como calcular o desvio padrão.
Exemplo 1: Para desvio padrão populacional
Encontre o desvio padrão da população de 8, 22, 26, 25, 30, e 33 .
Solução
Passo I: Encontre o significar dos dados populacionais fornecidos.
Média dos dados populacionais = Σx/n
= [8 + 22 + 26 + 25 + 30 + 33]/6
= 144/6
= 24
Etapa II: Agora encontre a distância típica de cada ponto de dados e distância. a média e o quadrado de cada desvio.
| Valores de dados (x eu Cura | x eu - µ | (x eu - µ) 2 |
| 8 | 8 - 24 = -16 | (-16) 2 = 256 |
| 22 | 22 - 24 = -2 | (-2) 2 = 4 |
| 26 | 26 - 24 = 2 | (2) 2 = 4 |
| 25 | 25 - 24 = 1 | (1) 2 = 1 |
| 30 | 30 - 24 = 6 | (6) 2 = 36 |
| 33 | 33 - 24 = 9 | (9) 2 = 81 |
Etapa III: Adicione os desvios para encontrar a soma estatística dos quadrados.
Σ(xi - µ) 2 = 256 + 4 + 4 + 1 + 36 + 81
Σ(xi - µ) 2 = 382
Etapa IV: Agora divida a soma dos quadrados por n .
Σ(xi - µ) 2 /n = 382/6
Σ(xi - µ) 2 /n = 63,667
Etapa V: Tire a raiz quadrada.
√[Σ(xi - µ) 2 /n] = √63,667
√[Σ(xi - µ) 2 /n] = 7,979
Use a calculadora de desvio padrão populacional acima para resolver esse problema rapidamente.
Exemplo 2: Para um desvio padrão da amostra
Encontre o desvio padrão de amostra de 12, 15, 18, 20, 25 .
Solução
Etapa I: Encontre a média dos dados de amostra fornecidos.
Média dos dados amostrais = Σx/n
= [12 + 15 + 18 + 20 + 25]/5
= 90/5
= 18
Etapa II: Agora encontre a distância típica de cada ponto de dados e distância. a média e o quadrado de cada desvio.
| Valores de dados (x eu ) | x eu - x̅ | (x eu -x̅) 2 |
| 12 | 12 - 18 = -6 | (-6) 2 = 36 |
| 15 | 15 - 18 = -3 | (-3) 2 = 9 |
| 18 | 18 - 18 = 0 | (0) 2 = 0 |
| 20 | 20 - 18 = 2 | (2) 2 = 4 |
| 25 | 25 - 18 = 7 | (7) 2 = 49 |
Etapa III: Adicione os desvios para encontrar a estatística soma dos quadrados .
Σ(xi - x̅) 2 = 36 + 9 + 0 + 4 + 49
Σ(xi - x̅) 2 =98
Etapa IV: Agora divida a soma dos quadrados por n – 1 .
Σ(xi - x̅) 2 / n-1 = 98/5-1
Σ(xi - x̅) 2 / n-1 = 98/4
Σ(xi - x̅) 2 / n-1 = 24,5
Etapa V: Tire a raiz quadrada.
√ [σ (xi - x̅) 2 /n-1] = √24,5
√[Σ(xi - x̅) 2 /n-1] = 4,95

