To calculate result you have to disable your ad blocker first.
Standard deviation calculator
Enter sample or population data in the given input box to find standard deviation using standard deviation calculator.
Standard deviation calculator
Standard deviation calculator is used to find the standard deviation, variance, mean, and the statistical sum of squares. This deviation calculator takes a sample and population set of data values.
What is the standard deviation?
The measure of the spread of data distribution is known as standard deviation. It measures the distance between each data observation and the mean. The standard deviation is of two types:
- Sample standard deviation
- Population standard deviation
If the given data is the population of its own, then divide the sum of squares by N.
If the given data is a sample from a larger population, then the sum of squares must be divided by n – 1.
Standard deviation formula
The formula for the population standard deviation is:
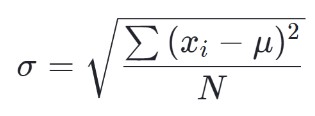
The formula for the sample standard deviation is:
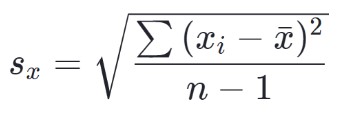
How to calculate standard deviation?
Below are a few solved examples to understand how to calculate standard deviation.
Example 1: For population standard deviation
Find the population standard deviation of 8, 22, 26, 25, 30, and 33.
Solution
Step I: Find the mean of the given population data.
Mean of population data = Σx/n
= [8 + 22 + 26 + 25 + 30 + 33]/6
= 144/6
= 24
Step II: Now find the typical distance of each data point & the mean and square of each deviation.
| Data values (xi) | xi - µ | (xi - µ)2 |
| 8 | 8 – 24 = -16 | (-16)2 = 256 |
| 22 | 22 – 24 = -2 | (-2)2 = 4 |
| 26 | 26 – 24 = 2 | (2)2 = 4 |
| 25 | 25 – 24 = 1 | (1)2 = 1 |
| 30 | 30 – 24 = 6 | (6)2 = 36 |
| 33 | 33 – 24= 9 | (9)2 = 81 |
Step III: Add the deviations to find the statistical sum of squares.
Σ(xi - µ)2 = 256 + 4 + 4 + 1 + 36 + 81
Σ(xi - µ)2 = 382
Step IV: Now divide the sum of squares by n.
Σ(xi - µ)2/n = 382/6
Σ(xi - µ)2/n = 63.667
Step V: Take the square root.
√[Σ(xi - µ)2/n] = √63.667
√[Σ(xi - µ)2/n] = 7.979
Use the population standard deviation calculator above to solve this problem quickly.
Example 2: For sample standard deviation
Find the sample standard deviation of 12, 15, 18, 20, 25.
Solution
Step I: Find the mean of the given sample data.
Mean of sample data = Σx/n
= [12 + 15 + 18 + 20 + 25]/5
= 90/5
= 18
Step II: Now find the typical distance of each data point & the mean and square of each deviation.
| Data values (xi) | xi - x̅ | (xi - x̅)2 |
| 12 | 12 – 18 = -6 | (-6)2 = 36 |
| 15 | 15 – 18 = -3 | (-3)2 = 9 |
| 18 | 18 – 18 = 0 | (0)2 = 0 |
| 20 | 20 – 18 = 2 | (2)2 = 4 |
| 25 | 25 – 18 = 7 | (7)2 = 49 |
Step III: Add the deviations to find the statistical sum of squares.
Σ(xi - x̅)2 = 36 + 9 + 0 + 4 + 49
Σ(xi - x̅)2 = 98
Step IV: Now divide the sum of squares by n – 1.
Σ(xi - x̅)2 / n-1 = 98/5-1
Σ(xi - x̅)2 / n-1 = 98/4
Σ(xi - x̅)2 / n-1 = 24.5
Step V: Take the square root.
√[Σ(xi - x̅)2 /n-1] = √24.5
√[Σ(xi - x̅)2 /n-1] = 4.95

