To calculate result you have to disable your ad blocker first.
Calcolatore Derivate
Inserisci la funzione, seleziona la variabile e fai clic sul pulsante Calcola per trovare la derivata utilizzando il calcolatore derivate.
Calcolatore Derivate
Il calcolatore della derivativa viene utilizzato per trovare la derivata di una determinata funzione rispetto alla variabile indipendente. Questa calcolatrice può eseguire una differenziazione esplicita con un solo clic.
Derivato: Definizione
Lascia che f(x) essere una funzione il cui dominio contiene un intervallo aperto in un punto X 0 . La funzione f(x) si dice che sia differenziabile a X 0 , e il derivato di f(x) al X 0 è dato da:
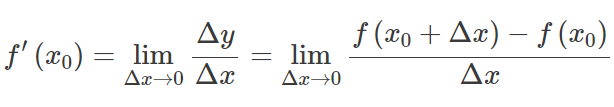
In altre parole, il derivato misura la sensibilità a un cambiamento nel valore della funzione rispetto a un cambiamento nel suo argomento. La funzione inversa della derivata è nota come antiderivativo.
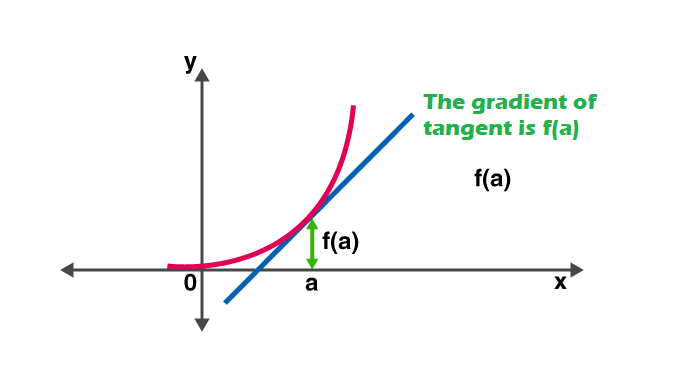
Regole della derivata
Ecco alcune regole di differenziazione:
Regola del potere
| f(x) | f'(x) |
| xn | nxn-1 |
Regole esponenziali
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
Regole logaritmiche
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
Regole trigonometriche
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
Regole di differenziazione
| f(x) | f'(x) |
| constant (c) | 0 |
| f(x) + h(x) | f'(x) + h'(x) |
| f(x) - h(x) | f'(x) - h'(x) |
| f(cx) | c * f'(x) |
| f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
Puoi avvalerti dell'aiuto del calcolatore di differenziazione di cui sopra per risolvere i problemi di differenziazione secondo le regole sopra discusse.
Come trovare i derivati utilizzando le regole?
Utilizza il nostro calcolatore di derivati con passaggi per differenziare le funzioni in base alle regole di differenziazione. Ecco un esempio manuale per differenziare una funzione utilizzando le regole.
Esempio
Trova la derivata della funzione data rispetto a "u".
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
Soluzione
Passo 1: Applicare d/du alla funzione data.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
Passo 2: Utilizza la regola del quoziente per differenziare l'espressione precedente.
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
Passaggio 3: Trova i derivati
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$ secondo la regola della somma
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
Passaggio 4: Ora sostituisci i risultati sopra in (1).
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Quindi,
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Esempi di derivati
Ecco alcuni esempi di derivate risolte dal nostro calcolatore di differenziazione.
| Funzione | Derivato della funzione |
| derivata di x | 1 |
| derivata di 3^x | 3 X * ln(3) |
| derivata di x^2 | 2x |
| derivata di x^1/2 | 1/x 1/2 |
| derivata di 5^x | 5 X * ln(5) |
| derivata di x/2 | 1/2 |
| derivata di x^e | e * x e-1 |
| derivata di 1/x | -1/x 2 |
| derivata di 2x | 2 |
| derivata di 2 | 0 |
| derivata di x^x | X X (ln(x) + 1) |
| derivata di x^-1 | -X -2 |
| derivata di 2^x | 2 X * ln(2) |
| derivata di 4^x | 4 X * ln(4) |
Puoi effettuare un controllo incrociato del risultato sopra utilizzando il nostro calcolatore di derivati.



