To calculate result you have to disable your ad blocker first.
Türev Hesaplayıcı
Türev hesaplayıcıyı kullanarak türevi bulmak için işlevi ve değişkeni girin.
Türev hesap makinesi
Türev hesap makinesi, belirli bir fonksiyonun bağımsız değişkene göre türevini bulmak için kullanılır. Bu hesap makinesi yalnızca tek bir tıklamayla açık bir farklılaşma gerçekleştirebilir.
Türev – Tanım
Hadi f(x) alanı bir noktada açık aralık içeren bir fonksiyon olsun X 0 . İşlev f(x) 'de diferansiyellenebilir olduğu söylenir X 0 , ve türevi f(x) at X 0 tarafından verilir:
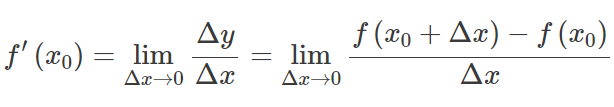
Başka bir deyişle türev, bağımsız değişkenindeki bir değişikliğe göre fonksiyon değerindeki bir değişikliğe karşı duyarlılığı ölçer. Türevin ters fonksiyonu antiderivatif.
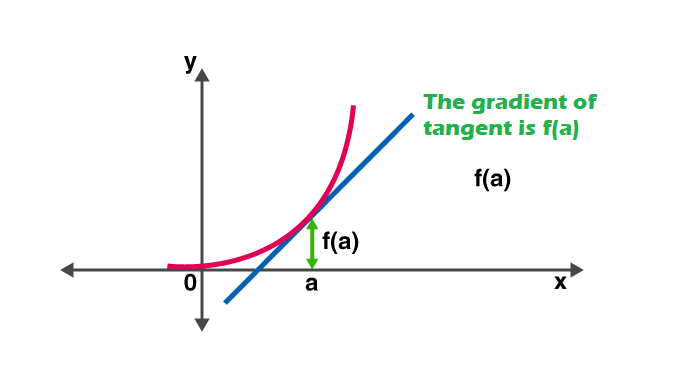
Türev Kuralları
İşte bazı farklılaşma kuralları:
Güç Kuralı
| f(x) | f'(x) |
| xn | nxn-1 |
Üstel Kurallar
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
Logaritmik Kurallar
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
Trigonometrik Kurallar
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
Farklılaştırma Kuralları
| f(x) | f'(x) |
| constant (c) | 0 |
| f(x) + h(x) | f'(x) + h'(x) |
| f(x) - h(x) | f'(x) - h'(x) |
| f(cx) | c * f'(x) |
| f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
Yukarıda tartışılan kurallara göre türev problemlerini çözmek için yukarıdaki türev hesaplayıcıdan yardım alabilirsiniz.
Kuralları kullanarak türevler nasıl bulunur?
Fonksiyonların türev alma kurallarına göre türevini almak için adımlarla türev hesaplayıcımızı kullanın. İşte bunun için manuel bir örnek bir fonksiyonun farklılaştırılması kuralları kullanmak.
Örnek
Verilen fonksiyonun "u"ya göre türevini bulun.
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
Çözüm
Aşama 1: Verilen fonksiyona d/du uygulayın.
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
Adım 2: Yukarıdaki ifadenin türevini almak için bölüm kuralını kullanın.
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
Aşama 3: Türevleri bulun
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
4. Adım: Şimdi yukarıdaki sonuçları (1)'de değiştirin.
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Dolayısıyla
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
Türev örnekleri
Burada türev alma hesaplayıcımız tarafından çözülen bazı türev örnekleri verilmiştir.
| İşlev | Fonksiyonun türevi |
| x'in türevi | 1 |
| 3^x'in türevi | 3x * ln(3) |
| x^2'nin türevi | 2x |
| x^1/2'nin türevi | 1/x1/2 |
| 5^x'in türevi | 5x * ln(5) |
| x/2'nin türevi | 1/2 |
| x^e'nin türevi | e * xe-1 |
| 1/x'in türevi | -1/x2 |
| 2x'in türevi | 2 |
| 2'nin türevi | 0 |
| x^x'in türevi | xx(ln(x) + 1) |
| x^-1'in türevi | -x-2 |
| 2^x'in türevi | 2x * ln(2) |
| 4^x'in türevi | 4x * ln(4) |
Türev hesaplayıcımızı kullanarak yukarıdaki sonucu çapraz kontrol edebilirsiniz.

