To calculate result you have to disable your ad blocker first.
เครื่องคำนวณอนุพันธ์
ป้อนฟังก์ชันและตัวแปรเพื่อค้นหาอนุพันธ์โดยใช้เครื่องคำนวณอนุพันธ์
เครื่องคำนวณอนุพันธ์
เครื่องคำนวณอนุพันธ์ใช้เพื่อค้นหาอนุพันธ์ของฟังก์ชันที่กำหนดเทียบกับตัวแปรอิสระ เครื่องคิดเลขนี้สามารถสร้างความแตกต่างที่ชัดเจนได้ในคลิกเดียว
อนุพันธ์ – คำนิยาม
ให้ ฉ(x) เป็นฟังก์ชันที่โดเมนมีช่วงเวลาเปิด ณ จุดใดจุดหนึ่ง x 0 . ฟังก์ชัน ฉ(x) ว่ากันว่า แตกต่าง ที่ x 0 , และ อนุพันธ์ ของ ฉ(x) ที่ x 0 มอบให้โดย:
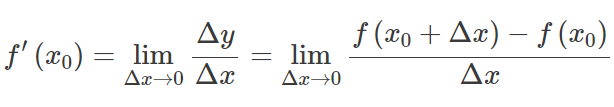
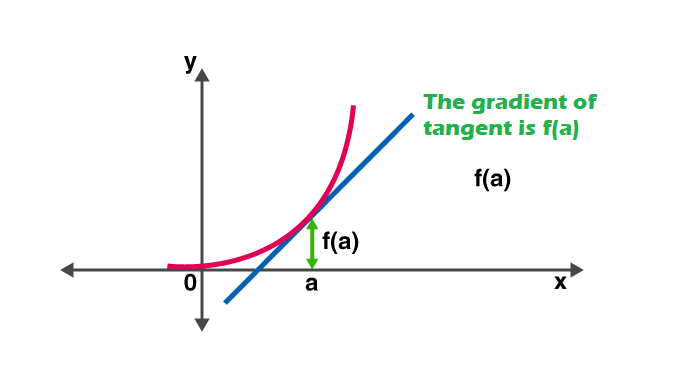
กล่าวอีกนัยหนึ่งอนุพันธ์วัดความไวต่อการเปลี่ยนแปลงของค่าฟังก์ชันที่เกี่ยวข้องกับการเปลี่ยนแปลงในการโต้แย้ง ฟังก์ชั่นย้อนกลับของอนุพันธ์เรียกว่า แอนติเดริเวทีฟ
กฎของอนุพันธ์
ต่อไปนี้เป็นกฎบางประการของการสร้างความแตกต่าง:
กฎแห่งอำนาจ
| f(x) | f'(x) |
| xn | nxn-1 |
กฎเอ็กซ์โปเนนเชียล
| f(x) | f'(x) |
| ax | ln(a) ax |
| ex | ex |
กฎลอการิทึม
| f(x) | f'(x) |
| loga(x) | 1/xln(a) |
| ln|x| | 1/x |
กฎตรีโกณมิติ
| f(x) | f'(x) |
| cos(x) | -sin(x) |
| sin(x) | cos(x) |
| tan(x) | sec2(x) |
| sec(x) | sec(x)tan(x) |
| csc(x) | -csc(x)cot(x) |
| cot(x) | -csc2(x) |
กฎความแตกต่าง
| f(x) | f'(x) |
| constant (c) | 0 |
| f(x) + h(x) | f'(x) + h'(x) |
| f(x) - h(x) | f'(x) - h'(x) |
| f(cx) | c * f'(x) |
| f(x) * h(x) | f'(x) h(x) + h'(x) f(x) |
| f(x) / h(x) | 1/h2(x)[f'(x) h(x) - h'(x) f(x)] |
คุณสามารถรับความช่วยเหลือจากเครื่องคำนวณหาความแตกต่างข้างต้นเพื่อแก้ไขปัญหาการหาความแตกต่างตามกฎที่กล่าวไว้ข้างต้น
จะหาอนุพันธ์โดยใช้กฎได้อย่างไร?
ใช้เครื่องคำนวณอนุพันธ์ของเราพร้อมขั้นตอนในการแยกฟังก์ชันตามกฎการหาอนุพันธ์ นี่คือตัวอย่างคู่มือสำหรับ การสร้างความแตกต่างให้กับฟังก์ชัน การใช้กฎเกณฑ์
ตัวอย่าง
ค้นหาอนุพันธ์ของฟังก์ชันที่กำหนดเทียบกับ "u"
$$f\left(u\right)=\frac{u}{\left(u^2+1\right)}$$
สารละลาย
ขั้นตอนที่ 1: ใช้ d/du กับฟังก์ชันที่กำหนด
$$\frac{d}{du}\left[f\left(u\right)\right]=\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]$$
ขั้นตอนที่ 2: ใช้กฎผลหารเพื่อแยกแยะนิพจน์ข้างต้น
$$=\frac{\left[\left(u^2+1\right)\:\frac{d}{du}\left(u\right)-u\:\frac{d}{du}\left(u^2+1\right)\right]}{\left(u^2+1\right)^2}$$ ... (1)
ขั้นตอนที่ 3: ค้นหาอนุพันธ์
$$\frac{d}{du}\left(u\right)=1$$
$$\frac{d}{du}\left(u^2+1\right)=\frac{d}{du}\left(u^2\right)+\frac{d}{du}\left(1\right)$$
$$\frac{d}{du}\left(u^2+1\right)=2u+0=2u$$
ขั้นตอนที่ 4: ตอนนี้แทนที่ผลลัพธ์ข้างต้นใน (1)
$$=\frac{\left[\left(u^2+1\right)\left(1\right)-u\left(2u\right)\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[u^2+1-2u^2\right]}{\left(u^2+1\right)^2}$$
$$=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
ดังนั้น
$$\frac{d}{du}\left[\frac{u}{\left(u^2+1\right)}\right]=\frac{\left[1-u^2\right]}{\left(u^2+1\right)^2}$$
ตัวอย่างของอนุพันธ์
ต่อไปนี้คือตัวอย่างอนุพันธ์บางส่วนที่แก้ได้ด้วยเครื่องคำนวณหาความแตกต่างของเรา
| การทำงาน | อนุพันธ์ของฟังก์ชัน |
| อนุพันธ์ของ x | 1 |
| อนุพันธ์ของ 3^x | 3x * ln(3) |
| อนุพันธ์ของ x^2 | 2x |
| อนุพันธ์ของ x^1/2 | 1/x1/2 |
| อนุพันธ์ของ 5^x | 5x * ln(5) |
| อนุพันธ์ของ x/2 | 1/2 |
| อนุพันธ์ของ x^e | e * xe-1 |
| อนุพันธ์ของ 1/x | -1/x2 |
| อนุพันธ์ของ 2x | 2 |
| อนุพันธ์ของ 2 | 0 |
| อนุพันธ์ของ x^x | xx(ln(x) + 1) |
| อนุพันธ์ของ x^-1 | -x-2 |
| อนุพันธ์ของ 2^x | 2x * ln(2) |
| อนุพันธ์ของ 4^x | 4x * ln(4) |
คุณสามารถตรวจสอบผลลัพธ์ข้างต้นได้โดยใช้เครื่องคำนวณอนุพันธ์ของเรา

